Trigonometry Solutions And Relationships Chart Table
The trigomertric principal inverses are listed in the following table.
Name |
Notation |
Definition |
Domain of x for real result |
Range of usual principal value ( radians) |
Range of usual principal value ( degrees ) |
| arcsine | y = arcsin x | x = sin y | −1 ≤ x ≤ 1 | − π /2 ≤ y ≤ π /2 | −90° ≤ y ≤ 90° |
| arccosine | y = arccos x | x = cos y | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| arctangent | y = arctan x | x = tan y | all real numbers | − π /2 < y < π /2 | −90° < y < 90° |
| arccotangent | y = arccot x | x = cot y | all real numbers | 0 < y < π | 0° < y < 180° |
| arcsecant | y = arcsec x | x = sec y | x ≤ −1 or 1 ≤ x | 0 ≤ y < π /2 or π /2 < y ≤ π | 0° ≤ y < 90° or 90° < y ≤ 180° |
| arccosecant | y = arccsc x | x = csc y | x ≤ −1 or 1 ≤ x | − π /2 ≤ y < 0 or 0 < y ≤ π /2 | -90° ≤ y < 0° or 0° < y ≤ 90° |
(Note: Some authors define the range of arcsecant to be ( 0 ≤ y < π /2 or π ≤ y < 3 π /2 ), because the tangent function is nonnegative on this domain. This makes some computations more consistent. For example using this range, tan(arcsec( x ))=√ x 2 -1 , whereas with the range ( 0 ≤ y < π /2 or π /2 < y ≤ π ), we would have to write tan(arcsec( x ))=±√ x 2 -1 , since tangent is nonnegative on 0 ≤ y < π /2 but nonpositive on π /2 < y ≤ π . For a similar reason, the same authors define the range of arccosecant to be ( - π < y ≤ - π /2 or 0 < y ≤ π /2 ).)
If x is allowed to be a complex number , then the range of y applies only to its real part.
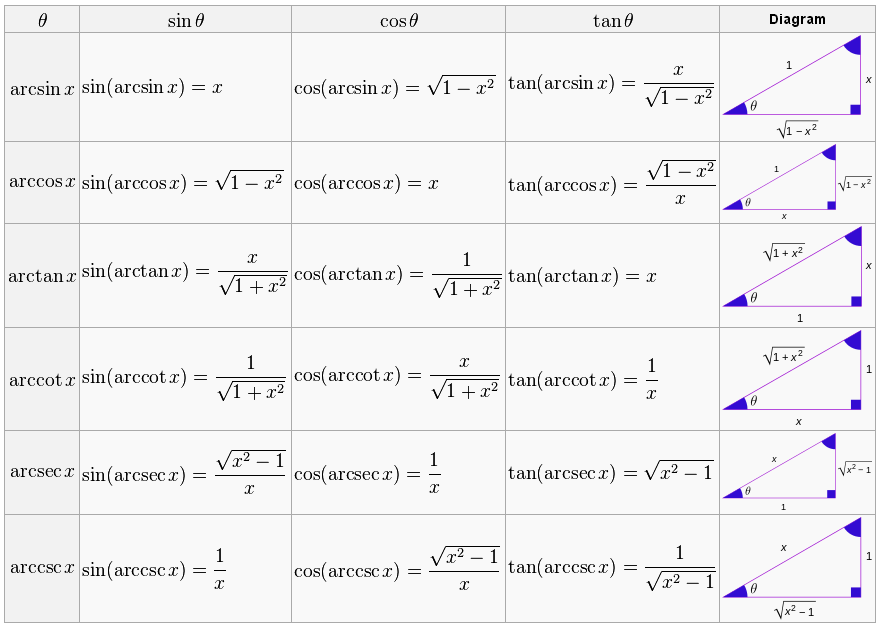
Relationships between trigonometric functions and inverse trigonometric functionsTrigonometric functions of inverse trigonometric functions are tabulated below. A quick way to derive them is by considering the geometry of a right-angled triangle, with one side of length 1, and another side of length x (any real number between 0 and 1), then applying the Pythagorean theorem and definitions of the trigonometric ratios. Purely algebraic derivations are longer.
Click on image below to enlarge