W-Flange Overhead Monorail Beam Analysis Calculator

MONORAIL BEAM ANALYSIS
For W-shaped Underhung Monorails Analyzed as Simple-Spans with / without Overhang
Per AISC 9th Edition ASD Manual and CMAA Specification No. 74 (2004)
Input:

Monorail Size:
Select:
Design Parameters:
Beam Fy =		ksi
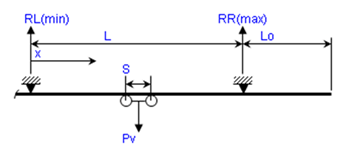
Beam Simple-Span, L =		ft.
Unbraced Length, Lb =		ft.
Bending Coef., Cb =	From AISC 9th Edition ASD Manual, page 5-47: Cb = 1.75+1.05(M1/M2)+0.3(M1/M2) <= 2.3 where: M1/M2 = ratio of smaller to larger bending moment at ends of the unbraced length, 'Lb'.
Overhang Length, Lo =		ft.
Unbraced Length, Lbo =	The unbraced length for the overhang (cantilever) portion, 'Lbo', is often debated. Here are some recommendations from different sources: 1. Per Fluor Enterprises Guideline 000.215.1257 - "Hoisting Facilities" Lbo = Lo+L/2 2. Per Dupont Standard DB1X - "Design and Installation of Monorail Beams" Lbo = 3Lo 3. Per ANSI MH27.1 - "Underhung Cranes and Monorail Systems" Lbo = 2Lo 4. Per British Steel Code B.S. 449, pages 42-44 (1959) Lbo = 2Lo (for top flange of monorail beam restrained at support) Lbo = 3Lo (for top flange of monorail beam unrestrained at support) 5. Per AISC Journal article by N. Stephen Tanner - "Allowable Bending Stresses for Overhanging Monorails" (3rd Quarter, 1985) Lbo = Lo+L (used with a computed value of 'Cbo' from article)	ft.
Bending Coef., Cbo =
Lifted Load, P =		kips	A =		in.^2	d/Af =
Trolley Weight, Wt =		kips	d =		in.	Ix =		in.^4
Hoist Weight, Wh =		kips	tw =		in.	Sx =		in.^3
Vert. Impact Factor, Vi =		%	bf =		in.	Iy =		in.^4
Horz. Load Factor, HLF =		%	tf =		in.	Sy =		in.^3
Total No. Wheels, Nw =			k=		in.	J =		in.^4
Wheel Spacing, S =		ft.	rt =		in.	Cw =		in.^6
Distance on Flange, a =		in.
			Support Reactions:
Results:			RR(max) =	For a monorail consisting of a simple-span with no overhang, 'RR(max)' and 'RL(min)' are determined by positioning the trolley at the right support. For a monorail consisting of a simple-span with an overhang, 'RR(max)' and 'RL(min)' are determined by positioning the trolley at the end of the overhang. The self-weight of the monorail beam is also included.
			RL(min) =	For a monorail consisting of a simple-span with no overhang, 'RR(max)' and 'RL(min)' are determined by positioning the trolley at the right support. For a monorail consisting of a simple-span with an overhang, 'RR(max)' and 'RL(min)' are determined by positioning the trolley at the end of the overhang. The self-weight of the monorail beam is also included.
Parameters and Coefficients:
Pv =	kips
Pw =	kips/wheel
Ph =	kips
ta =	in.
l =		l = 2*a/(bf-tw)
Cxo =		Cxo = -2.110+1.977l+0.0076e^(6.53*l)
Cx1 =		Cx1 = 10.108-7.408l-10.108e^(-1.364*l)
Czo =		Czo = 0.050-0.580l+0.148e^(3.015*l)
Cz1 =		Cz1 = 2.230-1.490l+1.390e^(-18.33*l)

Bending Moments for Simple-Span:
x =	ft.
Mx =	ft-kips
My =	ft-kips

Lateral Flange Bending Moment from Torsion for Simple-Span:					(per USS Steel Design Manual, 1981)
e =	in.
at =
Mt =	ft-kips

X-axis Stresses for Simple-Span:
fbx =	ksi				SR =
Lb/rt =
Fbx =	ksi

							(continued)
Y-axis Stresses for Simple-Span:
fby =	ksi
fwns =	ksi
fby(total) =	ksi
Fby =	ksi

						SR =
Combined Stress Ratio for Simple-Span:
S.R. =
						SR =
Vertical Deflection for Simple-Span:
Pv =	kips
D(max) =	in.	D(max) =
D(ratio) =		D(ratio) = L*12/D(max)
D(allow) =	in.	D(allow) = L*12/450

					SR =

Bending Moments for Overhang:
Mx =	ft-kips
My =	ft-kips

Lateral Flange Bending Moment from Torsion for Overhang:					(per USS Steel Design Manual, 1981)
e =	in.
at =
Mt =	ft-kips

X-axis Stresses for Overhang:
fbx =	ksi
Lbo/rt =
Fbx =	ksi

						SR =
Y-axis Stresses for Overhang:
fby =	ksi
fwns =	ksi
fby(total) =	ksi
Fby =	ksi

						SR =
Combined Stress Ratio for Overhang:
S.R. =

						SR =

Vertical Deflection for Overhang:
Pv =	kips
D(max) =	in.	D(max) =
D(ratio) =		D(ratio) = Lo*12/D(max)
D(allow) =	in.	D(allow) = Lo*12/450

					SR =
Bottom Flange Bending (simplified):
be =	in.
am =	in.
Mf =	in.-kips
Sf =	in.^3
fb =	ksi
Fb =	ksi

				SR =

Bottom Flange Bending per CMAA Specification No. 74 (2004):					(Note: torsion is neglected)

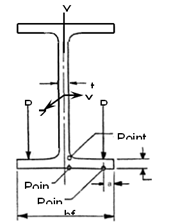
Local Flange Bending Stress @ Point 0:			(Sign convention: + = tension, - = compression)
sxo =	ksi	sxo = Cxo*Pw/ta^2
szo =	ksi	szo = Czo*Pw/ta^2

Local Flange Bending Stress @ Point 1:
sx1 =	ksi	sx1 = Cx1*Pw/ta^2
sz1 =	ksi	sz1 = Cz1*Pw/ta^2

Local Flange Bending Stress @ Point 2:
sx2 =	ksi	sx2 = -sxo
sz2 =	ksi	sz2 = -szo

Resultant Biaxial Stress @ Point 0:
sz =	ksi	sz = fbx+fby+0.75*szo
sx =	ksi	sx = 0.75*sxo
txz =	ksi	txz = 0 (assumed negligible)
sto =	ksi	sto = SQRT(sx^2+sz^2-sxsz+3txz^2)

						SR =
Resultant Biaxial Stress @ Point 1:
sz =	ksi	sz = fbx+fby+0.75*sz1
sx =	ksi	sx = 0.75*sx1
txz =	ksi	txz = 0 (assumed negligible)
st1 =	ksi	st1 = SQRT(sx^2+sz^2-sxsz+3txz^2)

						SR =
Resultant Biaxial Stress @ Point 2:
sz =	ksi	sz = fbx+fby+0.75*sz2
sx =	ksi	sx = 0.75*sx2
txz =	ksi	txz = 0 (assumed negligible)
st2 =	ksi	st2 = SQRT(sx^2+sz^2-sxsz+3txz^2)

						SR =