Elastomeric Bearing Pad Equations

Related Resources: bearing

Elastomeric Bearing Pad Equations

Bearing Engineering and Applications
Machine Design Applications
Engineering and Design Applications

Elastomeric Bearing Pad Equations (for an approximation of displacement)

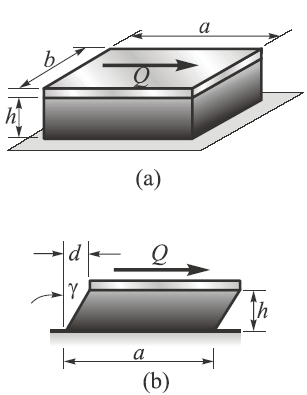
A bearing pad of the kind used to support machines and bridge girders consists of a linearly elastic material (usually an elastomer, such as rubber) capped by a steel plate (see figure (a)). Assume that the thickness of the elastomer is h, the dimensions of the plate are a · b , and the pad is subjected to a horizontal shear force Q.

Figure 1
Bearing pad in shear

Obtain formulas for the average shear stress aver τ in the elastomer and the horizontal displacement d of the plate (see figure (b)).

Assuming that the shear stresses in the elastomer are uniformly distributed throughout its entire volume. Then the shear stress on any horizontal plane through the elastomer equals the shear force Q divided by the area of the plane (see figure (a)):

Equation 1
τ_aver = Q / ( a · b )

The corresponding shear strain (from Hooke's law in shear, which will be considered below) is:

Equation 2
γ = τ_aver / G_e = Q / ( a · b · G_e)

in which e G_e is the shear modulus of the elastomeric material. Finally, the horizontal displacement d is equal to h · tan γ:

Equation 3
d = h · tan [ Q / ( a · b · G_e) ] = h · tan γ

In most practical situations the shear strain γ is a small angle, and in such cases we may replace tan γ by γ and obtain:

Equation 4
d = h · γ = h · Q / ( a · b · G_e )

Equations mentioned above give approximate results for the horizontal displacement of the plate because they are based upon the assumption that the shear stress and strain are constant throughout the volume of the elastomeric material. In reality the shear stress is zero at the edges of the material (because there are no shear stresses on the free vertical faces), and therefore the deformation of the material is more complex than pictured in the figure. However, if the length a of the plate is large compared with the thickness h of the elastomer, the results are satisfactory for design purposes.

References:

Stress-Strain State at a Point of Elastic Deformable Solid, 2010
Editor-in-Chief
Yakiv Karpov
Ministry of Education and Science Ukraine