Bolt Multiple Diameters Change of Length Under Axial Force Formula and Calculator

Related Resources: calculators

Bolt Multiple Diameters Change of Length Under Axial Force Formula and Calculator

Bolt & Screw Torque Charts and Equations

We also have to make some assumptions concerning cross-sectional areas of the bolt when computing change in length. The body area is no mystery; it’s merely equal to π D² / 4, where D is the nominal diameter of the fastener.

For the cross-sectional area of the threads, however, we must use the effective or ‘‘stress area’’.

Preview: Bolt Multiple Diameters Change of Length Under Axial Tension Loading Calculator

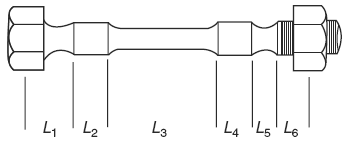
Bolt of multiple diameters, loaded in tension, and equivalent spring model
Figure 1 Each cross section of a complex fastener must be computed separately.

The combined change in length of the bolt will be equal to the sum of the changes in each section:

Equation 1
ΔL_c = ΔL₁ + ΔL₂ + ΔL₃ + ΔL_n...

Hooke’s law tells that the change in one section will be:

Equation 2
ΔL = (F · L ) / ( E · A )

Where

ΔL = change in length (in., mm)
A = cross-sectional area (in.², mm²)
L = length of the section (in., mm)
E = modulus of elasticity (psi, GPa)
F = applied tensile force (lb, N)

If the fastener has a more complex shape, as shown in Figure 1, then additional sections must be computed, but there is otherwise no change in the procedure.

Since the various sections are connected in series, they each see the same force, so we can combine Equations 1 and 2 above and write

Equation 3
ΔL_c = F_p [ L₁ / ( E A₁ ) + L₂ / ( E A₂ ) + L₃ / ( E A₃ ) + L₄ / ( E A₄ ) + L₅ / ( E A₅ ) + L₆ / ( E A₆ ) + L_n / ( E A_n ) + ...]

Where

ΔL_c = change in length of the body under load (in., mm) F
F_p = tension in bolt (lb, N)

Reference:

Introduction to the Design and Behavior of Bolted Joints Non-Gasketed Joints, Forth Edition
Founding Editor
L. L. Faulkner
Columbus Division, Battelle Memorial Institute,
Department of Mechanical Engineering
The Ohio State University
Columbus, Ohio