Related Resources: calculators
Lames equation Thick-walled Cylinders Formula and Calculator
Fluids Engineering and Design
Pressure Vessels Design and Engineering
Thick-walled Cylinders of Brittle Material, Ends Open or Closed Formula and Calculator
Lamé’s equation is used to determine the wall thickness when cylinders of this type are subjected to internal pressure.
Pressure. In designing a cylinder to
withstand internal pressure, the choice of formula to be used depends on:
1) the kind of
material of which the cylinder is made (whether brittle or ductile);
2) the construction of
the cylinder ends (whether open or closed); and
3) whether the cylinder is classed as a
thin- or a thick-walled cylinder.
A cylinder is considered to be thin-walled when the ratio of wall thickness to inside diameter is 0.1 or less and thick-walled when this ratio is greater than 0.1. Materials such as cast iron, hard steel, and cast aluminum are considered to be brittle materials; low-carbon steel, brass, bronze, etc. are considered to be ductile.
Preview: Lamé’s equation thick-walled cylinders of brittle material Calculator
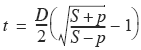
Where:
p = internal pressure, psi;
D = inside diameter of cylinder,
inches;
t = wall thickness of cylinder, inches;
S = allowable tensile stress, psi.
If metric SI units are used, then:
p = internal pressure in newtons per square meter
D = internal diameter of shell in meter
S = safe tensile stress in newtons per square meter
t = thickness of metal in the shell, in meter
The table Ratio of Outside Radius to Inside Radius, Thick Cylinders below is for convenience in calculating the dimensions of cylinders under high internal pressure without the use of Lames Equation.
Allowable Stress per Sq. In. of Section |
Working Pressure in Cylinder, Pounds per Square Inch |
||||||||||||
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
5000 |
5500 |
6000 |
6500 |
7000 |
|
2000 |
1.732 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2500 |
1.528 |
2.000 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
3000 |
1.414 |
1.732 |
2.236 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
3500 |
1.342 |
1.581 |
1.915 |
2.449 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
4000 |
1.291 |
1.483 |
1.732 |
2.082 |
2.646 |
… |
… |
… |
… |
… |
… |
… |
… |
4500 |
1.254 |
1.414 |
1.612 |
1.871 |
2.236 |
2.828 |
… |
… |
… |
… |
… |
… |
… |
5000 |
1.225 |
1.363 |
1.528 |
1.732 |
2.000 |
2.380 |
3.000 |
… |
… |
… |
… |
… |
… |
5500 |
1.202 |
1.323 |
1.464 |
1.633 |
1.844 |
2.121 |
2.517 |
3.162 |
… |
… |
… |
… |
… |
6000 |
1.183 |
1.291 |
1.414 |
1.558 |
1.732 |
1.949 |
2.236 |
2.646 |
3.317 |
… |
… |
… |
… |
6500 |
… |
1.265 |
1.374 |
1.500 |
1.648 |
1.826 |
2.049 |
2.345 |
2.769 |
3.464 |
… |
… |
… |
7000 |
… |
1.243 |
1.342 |
1.453 |
1.581 |
1.732 |
1.915 |
2.145 |
2.449 |
2.887 |
3.606 |
… |
… |
7500 |
… |
1.225 |
1.314 |
1.414 |
1.528 |
1.658 |
1.813 |
2.000 |
2.236 |
2.550 |
3.000 |
3.742 |
… |
8000 |
… |
1.209 |
1.291 |
1.382 |
1.483 |
1.599 |
1.732 |
1.890 |
2.082 |
2.324 |
2.646 |
3.109 |
3.873 |
8500 |
… |
1.195 |
1.271 |
1.354 |
1.446 |
1.549 |
1.667 |
1.803 |
1.964 |
2.160 |
2.408 |
2.739 |
3.215 |
9000 |
… |
1.183 |
1.254 |
1.330 |
1.414 |
1.508 |
1.612 |
1.732 |
1.871 |
2.035 |
2.236 |
2.490 |
2.828 |
9500 |
… |
… |
1.238 |
1.309 |
1.387 |
1.472 |
1.567 |
1.673 |
1.795 |
1.936 |
2.104 |
2.309 |
2.569 |
10,000 |
… |
… |
1.225 |
1.291 |
1.363 |
1.441 |
1.528 |
1.624 |
1.732 |
1.856 |
2.000 |
2.171 |
2.380 |
10,500 |
… |
… |
1.213 |
1.275 |
1.342 |
1.414 |
1.494 |
1.581 |
1.679 |
1.789 |
1.915 |
2.062 |
2.236 |
11,000 |
… |
… |
1.202 |
1.260 |
1.323 |
1.390 |
1.464 |
1.544 |
1.633 |
1.732 |
1.844 |
1.972 |
2.121 |
11,500 |
… |
… |
1.192 |
1.247 |
1.306 |
1.369 |
1.438 |
1.512 |
1.593 |
1.683 |
1.784 |
1.897 |
2.028 |
12,000 |
… |
… |
1.183 |
1.235 |
1.291 |
1.350 |
1.414 |
1.483 |
1.558 |
1.641 |
1.732 |
1.834 |
1.949 |
12,500 |
… |
… |
… |
1.225 |
1.277 |
1.333 |
1.393 |
1.458 |
1.528 |
1.604 |
1.687 |
1.780 |
1.883 |
13,000 |
… |
… |
… |
1.215 |
1.265 |
1.318 |
1.374 |
1.435 |
1.500 |
1.571 |
1.648 |
1.732 |
1.826 |
13,500 |
… |
… |
… |
1.206 |
1.254 |
1.304 |
1.357 |
1.414 |
1.475 |
1.541 |
1.612 |
1.690 |
1.776 |
14,000 |
… |
… |
… |
1.198 |
1.243 |
1.291 |
1.342 |
1.395 |
1.453 |
1.515 |
1.581 |
1.653 |
1.732 |
14,500 |
… |
… |
… |
1.190 |
1.234 |
1.279 |
1.327 |
1.378 |
1.433 |
1.491 |
1.553 |
1.620 |
1.693 |
15,000 |
… |
… |
… |
1.183 |
1.225 |
1.268 |
1.314 |
1.363 |
1.414 |
1.469 |
1.528 |
1.590 |
1.658 |
16,000 |
… |
… |
… |
1.171 |
1.209 |
1.249 |
1.291 |
1.335 |
1.382 |
1.431 |
1.483 |
1.539 |
1.599 |
Example, Use of the Table: Assume that a cylinder of 10 inches inside diameter is to withstand a pressure of 2500 psi; the material is cast iron and the allowable stress is 6000 psi. To solve the problem, locate the allowable stress per square inch in the left-hand column of the table and the working pressure at the top of the columns. Then find the ratio between the outside and inside radii in the body of the table. In this example, the ratio is 1.558, and hence the outside diameter of the cylinder should be 10 × 1.558, or about 155⁄8 inches. The thickness of the cylinder wall will therefore be (15.58 − 10)/2 = 2.79 inches.
Reference: Machinerys Handbook 30th Edition
Related: