Wind Driven Rain Load Equation and Calculator

Related Resources: calculators

Wind Driven Rain Load Equation and Calculator

Wind Driven Rain Load Review, Equation and Calculator

The load from rain, especially wind-driven rain, is the main reason for moisture-related building failure. Because the requirements of sometimes costly rain-protection measures depend on the local climate, some countries have introduced regional driving rain classifications. Generally, coastal regions and those on the windward side of mountains receive the highest precipitation load. Areas of low rainfall do not have the potential for severe wind driven rain.

Regional precipitation and wind are significant factors in determining local wind-driven rain load, but local exposure conditions are of equal importance. A building in an open field receives a higher load than one sheltered by a forest or other buildings. A quantification of exposure conditions for walls depending on landscape, neighborhood, and building size and geometry can be found in the British Standard BS 8104 and in the European ISO/DIN Standard 15927-3:2006.

The average wind-driven rain load RD in open ground was investigated by Lacy (1965). It is estimated from normal rain RN and the wind velocity component v parallel to the considered orientation:

R_d = f · v · R_N

Where:

R_d = wind-driven rain intensity, lb/ft²·h
f = empirical factor = approximately 0.06 s/ft
v = mean wind velocity, ft/s (or mph)
R_N = rain intensity on a horizontal surface in open field, lb/ft²·h

Conversion:

1 mph = 1.46667 ft/sec

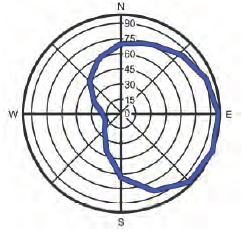
The image below shows a “rain rose” of results from Equation above plotted in polar coordinates indicating the amount of wind-driven rain in mass per unit area hitting an unobstructed and isolated vertical surface in the open field.

rain rose

Reference:

ASHRAE Fundamental Handbook, 2019