Related Resources: civil engineering
Bearing Capacity of Soil Equation and Calculator
Soil Bearing Capacity Equation and Calculator
Related: Bearing Capacity of Soils Analysis Document
Preview Soil Bearing Capacity Calculator
The approximate ultimate bearing capacity under a long footing at the surface of a soil is given by Prandtl's equation:
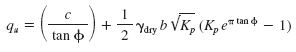
Where:
qu = Ultimate bearing capacity of soil, lb/ft2 (kg/m2)
c = Soil cohesion, lb/ft2 (kg/m2)
Φ = Angle of internal friction, degree
γdry = Unit weight of dry soil, lb/ft3 (kg/m3)
b = Width of footing, ft (m)
d = Depth of footing below surface, ft (m)
e = 2.718....
Kp = Coefficient of passive pressure
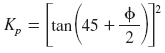
For footings below the surface, the ultimate bearing capacity of the soil may be modified by the factor 1 + Cd/b
The coefficient is about 2 for cohesionless soils and about 0.3 for cohesive soils. The increase in bearing capacity with depth for cohesive soils is often neglected.
Rankine Earth Pressure Coefficients
φ (deg) |
Rankine Ka |
Rankine Kp |
28 |
.361 |
2.77 |
30 |
.333 |
3.00 |
32 |
.307 |
3.26 |
The Coulomb active and passive earth pressure coefficient is derived from a more complicated expression that depends on the angle of the back of the wall, the soil-wall friction value and the angle of backfill. Although this expression is not shown, these values are readily obtained in textbook tables or by programmed computers and calculators. The Table shown below some examples of the Coulomb active and passive earth pressure coefficient for the specific case of a vertical back of wall angle and horizontal backfill surface. The Tables illustrate increasing soil-wall friction angles (δ).
Coulomb Active Pressure Coefficient
| φ (deg) |
δ (deg) |
||||
0 |
5 |
10 |
15 |
20 |
|
28 |
.3610 |
.3448 |
.3330 |
.3251 |
.3203 |
30 |
.3333 |
.3189 |
.3085 |
.3014 |
.2973 |
32 |
.3073 |
.2945 |
.2853 |
.2791 |
.2755 |
Coulomb Passive Pressure Coefficient
φ (deg) |
δ (deg) |
||||
0 |
5 |
10 |
15 |
20 |
|
30 |
3.000 |
3.506 |
4.143 |
4.977 |
6.105 |
35 |
3.690 |
4.390 |
5.310 |
6.854 |
8.324 |
Contributed by: Prashant Kien University of Montreal Pune, India