Fluid Pressure Drop Along Pipe Length of Uniform Diameter
Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
Pressure drop in pipes is caused by:
- Friction
- Vertical pipe difference or elevation
- Changes of kinetic energy
- Calculation of pressure drop caused by friction in circular pipes
To determine the fluid (liquid or gas) pressure drop along a pipe or pipe component, the following calculations, in the following order.
Equation Reynolds Number:
Re = ω D / v Re = ρ v l / µ Re = ω l / v Where: Re = Reynolds Number (unitless) Kinematic Viscosity Example kinematic viscosity values for air and water at 1 atm and various temperatures.Air Kinematic Viscosity m2/a
Water Kinematic Viscosity m2/ a
|
If the Reynolds number < 2320, than you have laminar flow.
Laminar flow is characterized by the gliding of concentric cylindrical layers past one another in orderly fashion. The velocity of the fluid is at its maximum at the pipe axis and decreases sharply to zero at the wall. The pressure drop caused by friction of laminar flow does not depend of the roughness of pipe.
If the Reynolds number > 2320, you have turbulent flow.
There is an irregular motion of fluid particles in directions transverse to the direction of the main flow. The velocity distribution of turbulent flow is more uniform across the pipe diameter than in laminar flow. The pressure drop caused by friction of turbulent flow depends on the roughness of pipe.
Select pipe friction Coefficient:
The pipe friction coefficient is a dimensionless number. The friction factor for laminar flow condition is a function of Reynolds number only, for turbulent flow it is also a function of the characteristics of the pipe wall.
Determine Pipe friction coefficient at laminar flow:
λ = 64 / Re
Where:
λ = Pipe Friction Coefficient
Re = Reynolds number
Note: Perfectly smooth pipes will have a roughness of zero.
Determine Pipe friction coefficient at turbulent flow (in the most cases) Colbrook Equation:
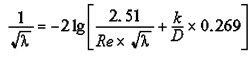
or
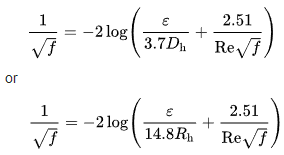
Where:
λ = Pipe Friction Coefficient
g = Acceleration of Gravity (9.8 m/s/s)
Re = Reynolds Number (unitless)
k = Absolute Roughness (mm)
D = Diameter of Pipe (m)
lg = Short for Log
The solutions to this calculation is plotted vs. the Reynolds number to create a Moody Chart.
Following table gives typical roughness values in millimeters for commonly used piping materials.
| Surface Material | Absolute Roughness Coefficient - k (mm) |
| Aluminum, Lead | 0.001 - 0.002 |
| Drawn Brass, Drawn Copper | 0.0015 |
| Aluminum, Lead | 0.001 - 0.002 |
| PVC, Plastic Pipes | 0.0015 |
| Fiberglass | 0.005 |
| Stainless steel | 0.015 |
| Steel commercial pipe | 0.045 - 0.09 |
| Stretched steel | 0.015 |
| Weld steel | 0.045 |
| Galvanized steel | 0.15 |
| Rusted steel | 0.15 - 4 |
| Riveted steel | 0.9 - 9 |
| New cast iron | 0.25 - 0.8 |
| Worn cast iron | 0.8 - 1.5 |
| Corroding cast iron | 1.5 - 2.5 |
| Asphalted cast iron | 0.012 |
| Galvanized iron | 0.015 |
| Smoothed cement | 0.3 |
| Ordinary concrete | 0.3 - 3 |
| Well planed wood | 0.18 - 0.9 |
| Ordinary wood | 5 |
Determine Pressure drop in circular pipes:
Δp = λ · L / D · ρ / 2 · ω2
Where:
Δp = Pressure Drop (Pa or kg / m-s 2)
λ = Pipe Friction Coefficient
L = Length of Pipe (m)
D = Pipe Diameter (m)
p = Density (kg/m3)
ω = Flow Velocity (m/s)
If you have valves, elbows and other elements along your pipe then you calculate the pressure drop with resistance coefficients specifically for the element. The resistance coefficients are in most cases found through practical tests and through vendor specification documents. If the resistance coefficient is known, than we can calculate the pressure drop for the element.
Δp = Γ · ρ / 2 · ω2
Where:
= Pressure Drop (kg/m2)
Γ = Resistance Coefficient (determined by test or vendor specification)
p = Density (kg/m3)
ω = Flow Velocity
Pressure drop by gravity or vertical elevation
Δp = ρ · g · ΔH
Where:
Δp = Pressure Drop
(kg/m2)
p = Density (kg/m3)
g = Acceleration of Gravity (9.8 m/s/s)
ΔH = Vertical Elevation or Drop
(m)
Pressure drop of gasses and vapor
Compressible fluids expands caused by pressure drops (friction) and the velocity will increase. Therefore is the pressure drop along the pipe not constant.
Where:
p1 = Pressure incoming (kg/m2)
T1 = Temperature incoming (°C)
p2 = Pressure leaving (kg/m2)
T2 = Temperature leaving (°C)
We set the pipe friction number as a constant and calculate it with the input-data. The temperature, which is used in the equation, is the average of entrance and exit of pipe.
Note: You can calculate gases as liquids, if the relative change of density is low (change of density/density = 0.02).
Related
- Head Loss Head loss is the reduction in the total head or pressure of the fluid as it moves through a fluid system.
- Friction Factor Friction factor has been determined to depend on the Reynolds number for the flow and the degree of roughness of the pipes
- Darcy's Equation Darcy's Equation Fluids Flow Equation - also called Darcy Weisbach equation.
- Minor Losses Pressure losses that occur in pipelines due to bends, elbows, joints, valves, etc. are sometimes called minor losses.
- Equivalent Piping Length Equivalent Piping Length Head Loss Equation Fluids
- Loss of Air Pressure Due To Pipe Friction Table 1 Loss of Air Pressure Due To Pipe Friction Table
- Loss of Air Pressure Due To Pipe Friction Table 2 Loss of Air Pressure Due To Pipe Friction Table
- Loss of Pressure Through Screw Pipe Fittings Loss of Pressure Through Screw Pipe Fitting. Each pipeline fitting within the system
- Hazen-Williams Method for Pipe Friction and Pressure Drop Hazen-Williams formula:
- Estimated Pressure Drop for Thermoplastic Lined Fittings and Valves Estimated Pressure Drop for Thermoplastic Lined Fittings and Valves.
Link to this Webpage:
© Copyright 2000 -
2024, by Engineers Edge, LLC
www.engineersedge.com
All rights reserved
Disclaimer |
Feedback
Advertising
| Contact
