Related Resources: fluid flow
Pressure Loss Across Louvers Equation and Calculator
Fluids Flow Design and Engineering
Hydraulic Pneumatic Design Engineering
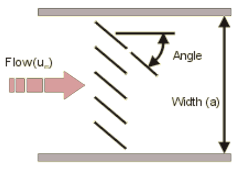
Head or pressure loss coefficient and head (pressure) loss of a fluid in across angled louvers inside a pipe equation and calculator.
ALL calculators require a Premium Membership
Preview: Pressure loss coefficient and head (pressure) loss across louvers calculator
The heat flow (q) from the plate is calculated as:
hL = kloss x (um2 / (2 x g) )
Where kloss is the head loss coefficient, um is the flow velocity in the pipe, and g is the gravitational acceleration. kloss is dependant on the Reynolds Number Re . If Re is smaller than or equal to 50, then (1 - 50 / Re) is taken to be zero:
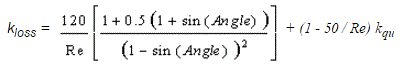
Where kqu is a function of the angle and the number of louvers based on a table of values (see table below), and Re is the Reynolds Number and is calculated as:
Re = um x Dh / v
Where:
N = Number of Louvers
A = Angle of louvers
a = Width (m)
g = 9.80665 m/s2
um = Flow Velocity in tube (m/s)
v = Kinematic Velocity (kg/m-s)
Dh = hydraulic diameter of the tube (m) - A square cross section has a hydraulic diameter equal to the width of the tube.
kqu = Angle vs Number of louver constant - see table below
kqu
|
↑
No. Louvers ↓ |
← Angle →
|
||||||||
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80 |
|
|
2
|
0.07
|
0.4
|
1.10
|
2.20
|
5.50
|
11.5
|
30.0
|
80.0
|
300.0
|
|
3
|
0.14
|
0.25
|
0.80
|
2.00
|
4.50
|
10.0
|
20.0
|
40.0
|
140.0
|
|
4
|
0.12
|
0.22
|
0.73
|
1.70
|
4.00
|
8.00
|
14.0
|
30.0
|
110.0
|
|
5
|
0.15
|
0.20
|
0.65
|
1.50
|
3.00
|
7.00
|
13.0
|
35.0
|
70.0
|
|
6
|
0.20
|
0.35
|
1.00
|
2.30
|
4.80
|
8.50
|
16.0
|
35.0
|
150.0
|
References
Idel'chik, I E. and Fried, Erwin., Flow Resistance, a Design Guide for Engineers , Taylor & Francis, Washington D.C. 1989. p 306.