Design of Load Carrying Shaft With One Pulley & Supported by Two Bearings

Mechanics and Machines Calculations Menu

Design of Load Carrying Shaft With One Pulley & Supported by Two Bearings

A belt pulley is keyed to the shaft, midway between the supporting bearings kept at 1000 mm apart. The shaft transmits 20 KW power at 400 rpm. Pulley has 400 mm diameter. Angle of wrap of belt on pulley is 180⁰ and the belt tensions act vertically downwards. The ratio of belt tensions = 2.5.

The shaft is made of steel having ultimate tensile stress and yield stress of 400 Mpa and 240 Mpa respectively. Use ASME code to design the diameter of shaft with combined fatigue and shock factors in bending and torsion as 1.5 and 1.25 respectively.

Machine Design Diagram:

Step I: Applying ASME code to find

Where:

= 0.3 x S_yt

OR

= 0.18 x S_ut

Whichever of the above two equations are minimum;

= 0.3 x 240 = 72 Mpa

OR

= 0.18 x 400 = 72 Mpa

Since, the pulleys are keyed to the shaft therefore, reducing smaller value by 25%.

= 0.75 x 72 = 54 Mpa

Step II : Torque Transmitted :

Using the relationship:

Since torque is transmitted by a belt drive:

Torque = (T₁ - T₂) r

477464.829 = (T₁ - T₂) x 200

(T₁ - T₂) = 2387.3241

also,

(2.5 T₂ - T₂) = 2387.3241

T₂ = 1591.5494,

Hence T₁ = 3978.8735 N

Step III - Find maximum B.M. i.e.; M:

Since belt tensions act vertically downwards, the vertical load at the center of the shaft becomes (T₁ + T₂ ) in the downward direction.

Therefore:

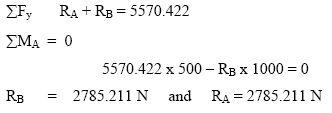
Bending moment Calculations:

B.M at A = 0

B.M at C = 2785.211 x 500 =1392605.644 Nmm

B.M at B = 0

Maximum Bending Moment (M_max) = 1392605.644 Nmm

Step IV - Using the final formula as per theory mentioned we find shaft diameter ‘d’

d³ = 204897.027

d = 58.9539 mm