Related Resources: pressure-vessel
Cone Cylinder Stress and Deflection Equations and Calculator
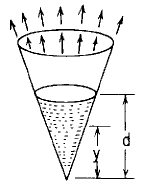
Cone Cylinder Stress and Deflection Filled to Depth with Liquid Tangential Edge Support Equation and Calculator. Per. Roarks Formulas for Stress and Strain for membrane stresses and deformations in thin-walled pressure vessels.
Preview: Cylinder Stress and Deflection Filled to Depth with Liquid Tangential Edge Support Calculator
|
Cone Cylindrical
|
At any level y below the liquid surface y < d
Meridional Stress
![]()
Circumferential or Hoop Stress
![]()
Radial Displacement of Circumference
![]()
Change in height dimension y
![]()
Rotation of a meridian from its unloaded position
![]()
At any level y above the liquid level
Note: There is a discontinuity in the rate of increase in fluid pressure at the top of the liquid. This leads to some bending in this region and is indicated by a discrepancy in the two expressions for the meridional slope at y = d.)
Meridional Stress
![]()
Circumferential or Hoop Stress
σ2 = 0
Radial Displacement of Circumference
![]()
Change in height dimension y
![]()
Rotation of a meridian from its unloaded position
![]()
Rotation of a meridian from its unloaded position
Where used:
E = Modulus of Elasticity (lbs/in2)
v = Poisson's ratio
δ = Liquid density (lbs/in3)
σ1,2 = stress, (lbs/in2)
y = At some level of the cone (in)
d = Liquid fill level, (in)
t = Wall thickness (in)
α = Angle (deg.)
ψ = Rotation of a meridian from its unloaded position, positive when that meridional rotation represents an increase in ΔR when y or θ increases;
Reference:
Roarks Formulas for Stress and Strain, 7th Edition