Related Resources: pressure-vessel
Spherical Cylinder Stress and Deflection Own weight Formula and Calculator
Spherical Cylinder Stress and Deflection Own weight, δ force/unit volume; tangential top edge support Equation and Calculator.
Per. Roarks Formulas for Stress and Strain for membrane stresses and deformations in thin-walled pressure vessels.
Preview: Spherical Cylinder Stress and Deflection Internal or External Pressure Calculator
|
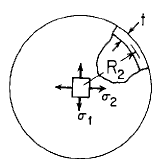
Spherical Cylinder
|
Own weight,
δ force/unit volume; tangential top edge support 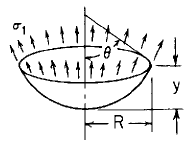 |
Deflection and Stress Own weight, δ force/unit volume; tangential top edge support.
For R2 / t > 10
Meridional Stress
![]()
Circumferential Hoop Stress
![]()
Maximum tensile stress
| at θ = 0° |
| σ2 = 0 | at θ = 51.83° |
Radial Displacement of Circumference
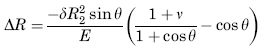
Change in height dimension y
![]()
Rotation of a meridian from its unloaded position
![]()
Where used:
E = Modulus of Elasticity (lbs/in2)
v = Poisson's ratio
δ = Density (lbs/in3)
σ1,2 = Stress, (lbs/in2)
R2 = Radius (in)
R = Distance as indicated (in)
y = Depth as indicated (in), Must be equal too or less than d
d = Depth of liquid (in)
t = Wall thickness (in)
θ = Angle (deg.)
ψ = Rotation of a meridian from its unloaded position, positive when that meridional rotation represents an increase in ΔR when y or θ increases;
(Note: There is a discontinuity in the rate of increase in fluid pressure at the top of the liquid. This leads to some bending in this region and is indicated by a discrepancy in the two expressions for the meridional slope at y = d.)
Reference:
Roarks Formulas for Stress and Strain, 7th Edition