Related Resources: vibration

Thin Flat Plates Uniform Thickness Natural Frequency Equations and Calculator

Machine Design and Engineering

Thin Flat Plates of Uniform Thickness Natural Frequency Equations and Calculator

ω_n = B [ ( E t² ) / ( ρ a⁴ ( 1 - v² )] ^(1/2)

Shape	Edge Conditions	B Value for Mode
		1	2	3	4	5	6	7	8
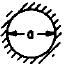	Clamped at Edge	11.84	24.61	40.41	46.14	103.12	-	-	-
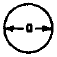	Free	6.09	10.53	14.19	23.80	40.68	44.68	61.38	69.44
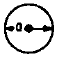	Clamped at Center	4.35	24.26	70.39	138.85	-	-	-	-
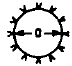	Simply Supported at Edge	5.90	-	-	-	-	-	-	-
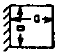	One Edge Clamped Three Edges Free	1.01	2.47	6.20	7.94	9.01	-	-	-
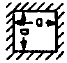	All Edges Clamped	10.40	21.21	31.29	38.04	38.22	47.73	-	-
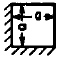	Two Edge Clamped Two Edges Free	2.01	6.96	7.74	13.89	18.25	-	-	-
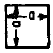	All Edges Free	4.07	5.94	6.91	10.39	17.80	18.28	-	-
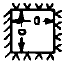	One Edge Clamped Three Edges Simply Supported	6.83	14.94	16.95	24.89	28.99	32.71	-	-
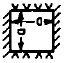	Two Edges Clamped Two Edges Simply Supported	8.37	15.82	20.03	27.34	29.54	37.31	-	-
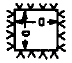	All Edges Simply Supported	5.70	14.26	22.82	28.82	37.08	48.49	-	-

Where:

E = Young's Modulus ( lb / in² ),
t = Thickness of Plate (in),
ρ = Mass Density (lb-sec² / in⁴)
a = Diameter of Circular Plate or Side of Square Plate (in),
v = Poisson's Ratio
B = Coefficient for given nodes from image table above,
ω_n = Angular Natural Frequency ( rad / sec )

Related and Useful Links:

• Poisson's Ratio
• AISC Steel Construction Shapes Properties Viewer
• Young's Modulus on Common Engineering Materials

Reference Harris, Shock and Vibration Handbook