Related Resources: beam bending
Double Integration Method Example 4 Proof Simply Supported Beam of Length L with Partial Distributed Load
Beams Deflection and Stress Formulas and Calculators
Engineering Mathematics
Double Integration Method Example 4 Proof Simply Supported Beam of Length L with Partial Distributed Load.
The Double Integration Method, also known as Macaulay’s Method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.
Elastic Curve
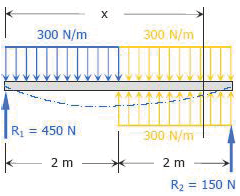
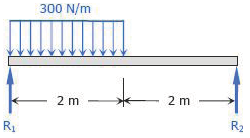
Compute the value of EI δ at midspan for the beam loaded as shown in the figure above. If E = 10 GPa, what value of I is required to limit the midspan deflection to 1/360 of the span?
∑ MR2 = 0
4 R1 = 300 ( 2 ) ( 3 )
R1 = 450 N
∑ MR1 = 0
4 R2 = 300 ( 2 ) ( 1 )
R2 = 150 N
E I y'' = 450 x - 0.5 (300) x2 + 0.5 (300) < x - 2 >2
E I y'' = 450 x - 150 x2 + 150 < x - 2 >2
E I y' = 225 x2 - 50 x3 + 50 < x - 2 >3 + C1
E I y = 75 x3 - 12.5 x4 + 12.5 < x - 2 >4 + C1 x + C2
At x = 0, y = 0, therefore C2 = 0
At x = 4 m, y = 0
0 = 75 (43) - 12.5 (44) + 12.5 ( 4 -2 )4 +4 C1
C1 = -450 N·m2
Therefore,
E I y = 75 x3 - 12.5 x4 + 12.5 < x - 2 >4 - 450 x
At x = 2 m (midspan)
E I ymidspan = 75 ( 23 ) - 12.5 ( 24) + 12.5 ( 2 - 2 )4 - 450 (2)
E I ymidspan = -500 N·m3
E I δmidspan = 500 N·m3
Maximum midspan deflection
δmidspan = L/360 = 4 / 360 = M / 90
δmidspan = ( 100 / 9 )
Thus,
10,000 I (100 / 9) = 500 ( 10003 )
I = 4,500,000 mm4 or
I = 4.5 x 106 mm4
Related:
- Double Integration Method for Beam Deflections
- Double Integration Method Example 1 Simply Supported Beam of Length L with Concentrated Load at Mid Span
- Double Integration Method Example 3 Proof Cantilevered Beam
- Beam Calculator Cantilevered Beam with One Load Applied at End Deflection and Stress Structural Beam Deflection, Stress, Bending Equations and calculator for a Cantilevered Beam with One Load Applied at End.
- Curved Beam Stress and Deflection Design Spreadsheet Calculator
- Curved Circular (Cylinder) Beam Stress Formulas and Calculator
Reference:
- Dr. ZM Nizam Lecture Notes
- Shingley Machine Design, 4-3 "Deflection Due to Bending"
- Beam Deflection by Integration Lecture Presentation Paul Palazolo, University of Memphis,
- Beam Deflections Using Double integration, Steven Vukazich, San Jose University