Concrete Modulus of Elasticity Equations and Calculator

Related Resources: calculators

Concrete Modulus of Elasticity Equations and Calculator

Civil Engineering and Design
Strength of Materials Basics and Equations | Mechanics of Materials

Concrete Secant Modulus of Elasticity Equations and Calculator

The modulus of elasticity (also known as Young’s modulus) is defined as the ratio of stress to strain in the elastic region. Unlike steel, the modulus of elasticity of concrete varies with compressive strength. Since the slope of the stress-strain curve varies with the applied stress, there are several ways of calculating the modulus of elasticity. Figure 1 shows a typical stress-strain curve for concrete with the initial modulus, the tangent modulus, and the secant modulus indicated.

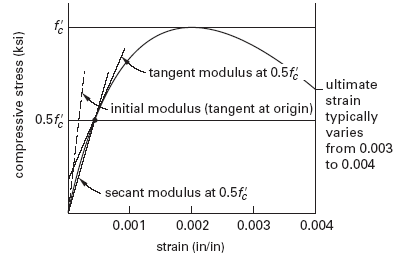
Figure 1, Concrete Stress Strain Curve

The secant modulus of elasticity is specified by ACI 318 for use with specific weights that are between 90 lbf/ft³ and 160 lbf/ft³ (1440 kg/m³ and 2560 kg/m³). Equation 1 & 2 are used for both instantaneous and long term deflection calculations. ω_c is in lbf/ft³(kg/m³), and E_c and f'_c are in lbf/in² (MPa) [ACI 318 Sec. 8.5.1].

Secant modulus of elasticity

Eq. 1, SI Units
E_c = 0.043 ω_c^1.55 (f'_c)^0.5

Eq. 2, U.S.
E_c = 33 ω_c^1.55 (f'_c)^0.5

For normal weight concrete, ACI 318 uses Eq. 3 & 4, which corresponds to a specific weight of approximately 145 lbf/ft³ (2320 kg/m³) [ACI 318 Sec. 8.5.1].

Eq. 3, SI
E_c = 5,000 (f'_c)^0.5

Eq. 4, U.S.
E_c = 57,000 (f'_c)^0.5

Where:

ω_c = specific weight, lbf/ft³(kg/m³)
f'_c = compressive strength of concrete, lbf/in² (MPa)
E_c = modulus of elasticity (young's modulus), lbf/in² (MPa)

Reference

Civil Engineering Reference Manual, Fifteenth Edition, Michael R. Lindeburg, PE