Related Resources: calculators

Hydraulic Jump Equations and Calculator

Civil Engineering and Design
Fluids Engineering and Design

Hydraulic Jump Conjugate Depths Equations and Calculator

If water is introduced at high (supercritical) velocity to a section of slow-moving (subcritical) flow (as shown in Fig. 1), the velocity will be reduced rapidly over a short length of channel. The abrupt rise in the water surface is known as a hydraulic jump. The increase in depth is always from below the critical depth to above the critical depth. The depths on either side of the hydraulic jump are known as conjugate depths.

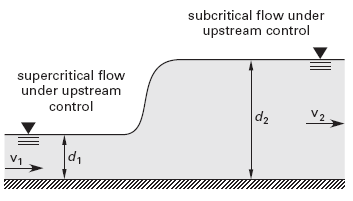
Hydraulic Jump Conjugate Depths
Figure 1 - Hydraulic Jump Conjugate Depths

Preview Hydraulic Jump Conjugate Depths Calculator

The conjugate depths and the relationship between them are as follows.

Eq.1 Rectangular Channels
d1 = - 0.5 · d2 + [ ( 2 · v22 d2 ) / g + d22 / 4 ]0.5

Eq. 2 Rectangular Channels
d2 = - 0.5 · d1 + [ ( 2 · v12 d1 ) / g + d12 / 4 ]0.5

Eq. 3 Rectangular Channels
d2 / d1 = 0.5 [ ( 1 + 8 · Fr12 ) -1 ]

Eq. 4 Rectangular Channels
d1 / d2 = 0.5 [ ( 1 + 8 · Fr22 ) -1 ]

If the depths d1 and d2 are known, then the upstream velocity can be found from

Eq. 5
v12 = [ ( g · d2 ) / ( 2 · d1 ) ] ( d1 + d2 )

Where:

d1 = downstream depth, ft, (m)
d2 = upstream depth, ft, (m)
v1 = downstream water velocity, ft/s, (m/s)
v2 = upstream water velocity, ft/s, , (m/s)
g = gravitational acceleration, 32.2 ft/sec2 (9.81 m/s2)
Fr1 = upstream Froude number dimensionless
Fr2 = downstream Froude number dimensionless

Conjugate depths are not the same as alternate depths. Alternate depths are derived from the conservation of energy equation (i.e., a variation of the Bernoulli equation). Conjugate depths are derived from a conservation of momentum equation. Conjugate depths are calculated only when there has been an abrupt energy loss such as occurs in a hydraulic jump or drop.

Hydraulic jumps have practical applications in the design of stilling basins. Stilling basins are designed to intentionally reduce energy of flow through hydraulic jumps. In the case of a concrete apron at the bottom of a dam spillway, the apron friction is usually low, and the water velocity will decrease only gradually. However, supercritical velocities can be reduced to much slower velocities by having the flow cross a series of baffles on the channel bottom.

Reference

Civil Engineering Reference Manual, Fifteenth Edition, Michael R. Lindeburg, PE

Related

Link to this Webpage:

Copy Text to clipboard

Spider Optimizer

© Copyright 2000 - 2024, by Engineers Edge, LLC
www.engineersedge.com
All rights reserved
Disclaimer | Feedback
Advertising | Contact