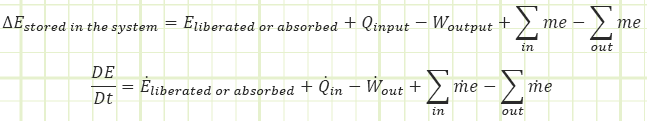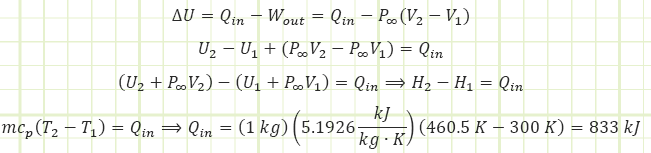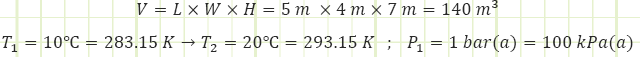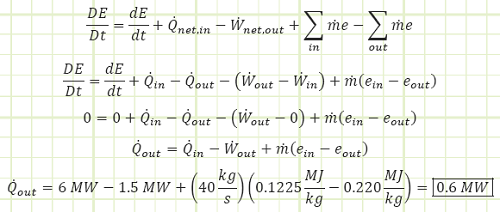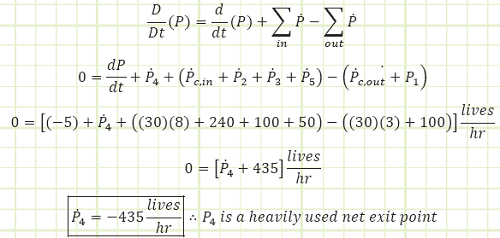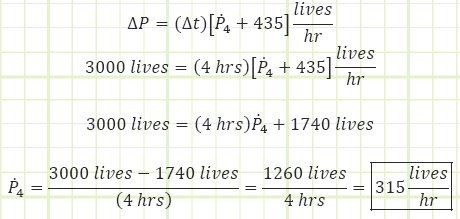Related Resources: thermodynamics

Control Volume Analysis Class 3

Thermodynamics Data, Equations, Charts, Equations and Calculators

Class 3 – Control Volume Analysis, Reynolds Transport Theorem, Conservation of Mass, and the First

Law of Thermodynamics

---

Objective(s):

At the completion of the lecture, students should:

1) Understand how to identify and delineate a system as a control volume.

2) Understand how to account for transport phenomena through the CV boundary as well as internal generation or elimination of a property within the CV.

3) Be able to apply a control volume analysis to a system in order to fully account for quantities of a property between different states bounded by a process (either through time or through space).

4) Understand the types of energy as a stored property.

5) Understand the methods by which energy can be transferred to/from a system.

6) Understand the application of First Law of Thermodynamics to a control volume via Reynolds Transport.

7) Recognize energy can have varying degrees of quality despite having equivalent quantity.

8) Apply specific heat capacity to determine the internal energy or enthalpy of a substance.

Methodology:

Lecture with tangible examples (human body as a control volume for mass, bank account as a control volume for money [deposits, withdrawals, interest, fees], a classroom as a control volume for people…), visual demonstration of filling one bottle via another while draining it at a different rate.

Terminology:

System: A place in space with a defined boundary, within which we care about the properties of its contents. Your body is a system that interacts with the surroundings by various transport phenomena, like eating, breathing, perspiring, getting cold, lifting/pushing/pulling, being warmed by sunlight etc.

Surroundings: Everything outside of the system. Generally, we don’t care about its mass, although its temperature and pressure could be very important.

Property: A characteristic of a system’s contents, such as pressure, temperature, volume, internal energy, etc. Can be independent of mass (pressure & temperature), which makes it an intensive property. An extensive property depends on the amount of substance there is (total energy, total volume). If we divide out the amount of mass, it becomes a specific quantity, such as m³/kg (i.e. specific volume, which is the inverse of density).

State: a stable condition in which a system is everywhere homogenous (isotropic) and therefore in equilibrium with itself. For simple compressible systems, knowing two intensive or specific properties completely specifies the overall state from which all the other intensive and specific properties can be determined. States describe a single point location on the overall 3D surface of all available states (see Lecture 2 for the Ideal Gas P-v-T surface).

Process: Something that causes a system’s state to change to a different state in which properties have changed. Thermodynamic processes are idealized as being done VERY slowly in order for every infinitesimally different intermediate state to be in equilibrium with itself. Heating, cooling, compressing, expanding, adding/subtracting mass, chemically reacting, lifting/dropping, accelerating, etc. are all processes that change the state of a system by following a certain path along the surface of available states.

Key Ideas:

Various types of control volumes:

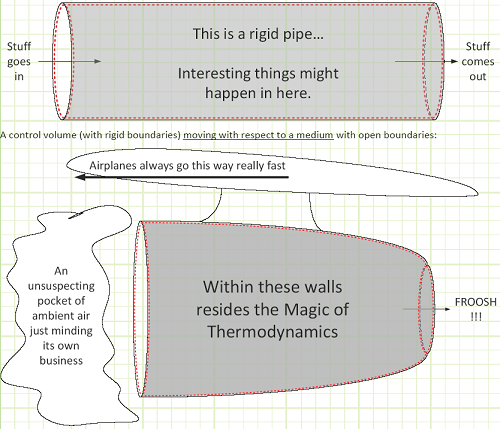
Fixed control volume (boundaries don’t change shape or size, so volume doesn’t change) with open boundaries (mass can flow in and out):

A deforming (and possibly also moving) control volume with part of its boundary open (allowing the expulsion of mass).

A deforming control volume with a closed boundary (mass is constant, but heat may cross the boundary to change its internal energy and the deformation may cause work interactions that will also change the internal energy):

 

A deforming control volume with a closed boundary (mass is constant, but work may cross the boundary via a spinning shaft and paddle to change its internal energy and the deformation may cause work interactions that will also change the internal energy):

 

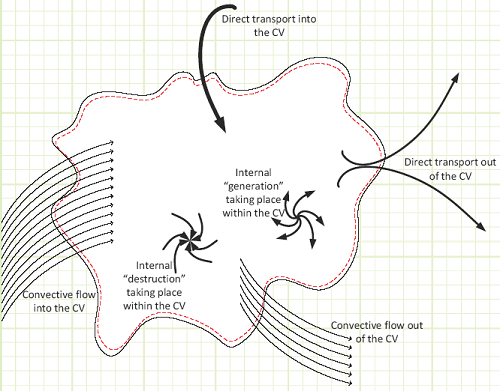
A general control volume, with all the means by which some studied property can be tracked.

The studied property, generically labeled “B,” can be tracked via the Reynolds Transport Theorem.

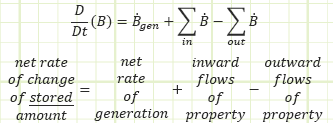
In words, the net rate of change of the studied property stored inside of our control volume equals the net rate at which the property is being generated (if negative, then there’s more destruction than creation), plus all the inflows, and minus all the outflows as a time-based flow rate.

Compare this to the property of dollars in a Roth IRA account offered by a brokerage firm:

Internal generation: your stored money accrues interest/dividends at a certain rate, maybe 5% per year.

Internal destruction: the firm charges management fees that automatically deduct from your balance at 0.5% per day.

Direct inflow: You deposit some amount of your hard-earned cash with the hope it’ll grow.

Direct outflow: You withdraw a few thousand G’s because the government has been shut down again and you’ve gone two pay periods without a paycheck and need to pay for

food/gas/electricity/water/clothes/dependents/school supplies/maintenance/cat food/mortgage

Convection flow: Your loving parents sympathize with you and gift some shares of General Electric stock, which carries with it a certain dollar amount per share of stock.

The Transport Theorem doesn’t need to be analyzed on a rate basis. It can be studied over a set period of time (multiply through by dt or Δt). This works really well for closed systems (i.e. constant mass) undergoing a process from one state to another.

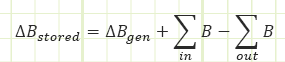
Conserved quantity - Mass:

It’s fairly well-known that in most practical cases mass is a conserved quantity. It seldom ever just materializes out of thin air or disappears without a trace, not counting weird stuff that happens in atomic nuclei. So, Reynold’s Transport works particularly well at accounting for the mass stored in a control volume.

If the control volume is closed to the flow of matter, it’s actually relabeled as a “Control Mass,” because its mass is invariant with time. Energy interactions through mechanisms of heat transfer or work may still occur.

If matter may cross the boundaries, it is an “open system” and we’re back to calling it a “Control Volume.” The amount of stored mass may change with regard to time. The matter coming in or leaving may also have energy associated with it.

In open systems, if the rate of change of the property in question, be it mass or energy, is not changing in time, then the system is considered to be at steady state.” If the amount of storage is changing in time, then the system is “transient” or “unsteady.”

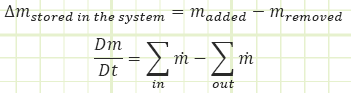
Conserved quantity - Momentum:

Momentum (angular and translational) is another famous conserved quantity. We’re not gonna say much more about it in this class, but it’s the bee’s knees in Fluids.

Conserved quantity – Energy (The First Law of Thermodynamics):

This is the main (and, along with momentum, the most fundamental) conserved quantity we’ll deal with in this class. Sometimes you may need to do a simultaneous analysis of both mass and energy to get a convergent answer for some of our thermo questions.

The premise here is the total energy in the universe remains constant. Whatever energy leaves our system (i.e. crosses the control volume boundaries) it must enter the surroundings. At no point can energy ever just cease to exist, it was to go or be somewhere. It also can’t just spring up from nothing. Energy comes in many forms: kinetic, potential (gravitational, electrical, intermolecular, nuclear, chemical, spring), thermal, etc. Energy can change forms, although the second law of thermo puts some constraints on this conversion process.

“E” is the total energy stored in the control volume and “e” is the total specific energy either entering or leaving the control volume by the movement of mass across its boundary.

“E” and “e” are composites of all the kinds of energy they can be representing or transporting. Typically, this is:

E = kinetic energy + potential energy + internal energy

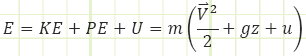
“e” is a little different from “E” because it must include the energy associated with flow (think Bernoulli’s Equation here, where there are KE and PE terms and a pressure term as well.

e = Bernoulli + internal energy = kinetic energy + potential energy + pressure energy + internal energy

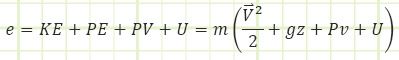
Kinetic energy: Energy associated with bulk organized motion (translating or rotating coherently).

Potential energy: Energy associated with position relative to a conservative force field.

Internal energy: Energy associated with random molecular motion. This is the important one in thermo!

Usually, but not always, KE and PE will be negligible because either velocity is relatively low or elevation changes are small. So, the most common E will just be equal to U and “e” will just be equal to U + PV.

This gives us a first law equation looking like:

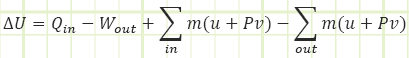
Since u+Pv will actually show up a lot, we lump it together as its own thing and name it “Enthalpy.” Enthalpy is just internal energy plus “flow energy” or “pressure energy” from the Bernoulli equation.

H = U - PV & h = u + Pv = u + P / ρ

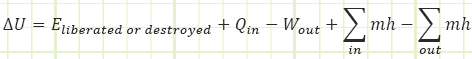
In the rate form, which we won’t use much for this first month, it looks like this:

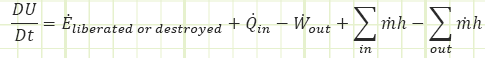
Isn’t energy conserved? How can it be liberated or destroyed? It can’t, but it may show up from unexpected places or hide itself in mysterious ways. The 𝐸̇_{𝑙𝑖𝑏𝑒𝑟𝑎𝑡𝑒𝑑} term is good at being a “catch all” for any sources of energy generation or extinction you didn’t think to look out for (like radioactive nuclear decay).

Nowhere in these equations do we see temperature mentioned, which is unfortunate, since it’s impossible to “measure” energy with some sort of gauge in the same way we easily measure pressure, volume, and temperature. So, it would be nice to relate energy to temperature. Let’s introduce two new properties: specific heat capacity for constant volume processes and specific heat capacity for constant pressure processes.

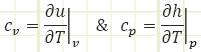
In words: specific heat capacity at constant volume is defined as the amount of internal energy gained or lost by a substance given a change in temperature during a process carried out at constant volume.

Specific heat capacity at constant pressure is defined as the amount of enthalpy gained or lost by a substance given a change in temperature during a process carried out at constant pressure.

Said another way, if you want temperature to increase, it’s the energy you need to add to get that change.

For liquids and solids, which are considered incompressible and therefore have a more-or-less constant volume, no distinction is necessary and the two specific heat capacities are equal.

The specific heat capacity of liquid water at room temperature is 4.18 kJ/kg·K. This means if we wanted to change the temperature of one kilogram of water by 1°C, we would need to add or subtract 4.18 kJ.

The value of specific heat capacity will change based upon the temperature of the substance…BUT, for this class, we will typically assume it remains constant. This can produce errors when the temperature of the substance being evaluated is very different from the temperature at which we referenced the value of specific heat capacity.

So how do we use them?

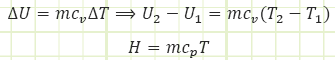
Make sure to always add the assumption that “specific heat remains constant during the process” when you use it to solve problems.

Physical interpretation of c_v:

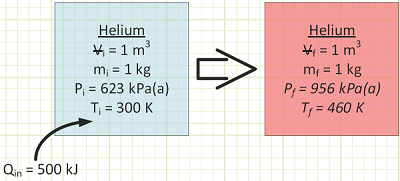
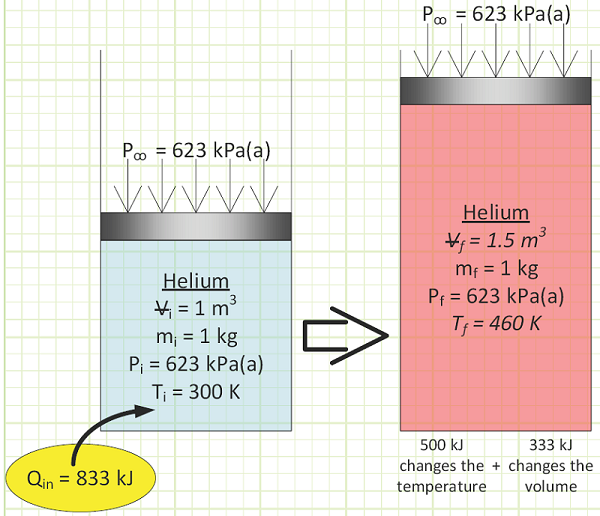
For He, c_v is taken from Appendix A-2 to be 3.1156 kJ/kg·K. At constant volume, the gas molecules can only fly around faster as energy is transferred to them via heat transfer. This is exhibited by a rise in Temperature.

Pressure also goes up, because the molecules hit the box’s walls harder. From the First Law for a Closed System:

ΔU = Q_in - W_out

There is no work associated with this, as there’s no pushing occurring over any distance (or expanding over a volume change), so W_out = 0.  

ΔU = Q_inΔ for this constant volume heating process

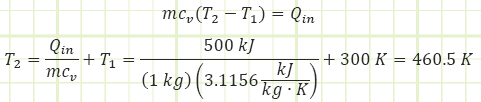
To get a temperature change of 160°C for our 1 kg of helium in a rigid box, we need to add 500 kJ of energy.

Physical interpretation of c_p:

If, instead of constant volume, pressure remains constant during an expansion process, some of the heat energy added to a closed system is used to push against a moving boundary. The gas expands outward, pushing against a force (or pressure).

Picture this: a gas molecule gains velocity at the bottom of a cylinder due to heat transfer, flies upward really quickly, then hits a movable piston. Some of its momentum will transfer to the piston and cause it to rise against ambient pressure. Therefore, the gas molecule loses some of its newfound speed to the piston to a new height. So it takes more added heat to raise the gas temperature by the same amount when it’s heated at constant pressure than it does when volume remains constant. Part of the heat turns into work.

To get the same temperature rise, 333 kJ more kJ needed to be added than in the isochoric case.

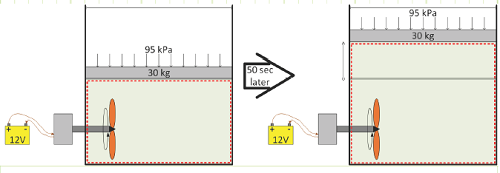
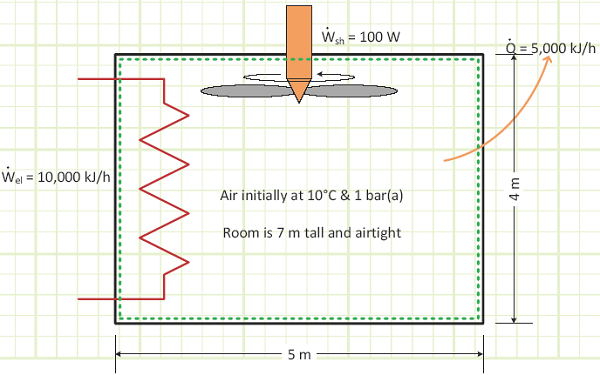
EXAMPLE 1 – TRANSIENT HEATING OF A SEALED ROOM

Problem statement: A sealed room containing air at 1 bar(a) is initially at 10°C. There is a fan running at 100 W, a resistance heater rated for 10,000 kJ/h, and imperfect insulation allowing heat to escape at a rate of 5,000 kJ/h. The room is 4 m x 5 m x 7 m. How long will it take [min & sec] for the air temperature to reach 20°C? What is the final pressure [kPa]?

Given:

Work interactions in/out of control volume.

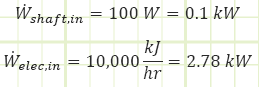
Heat interactions in/out of control volume.

Room geometry and contents.

Find:

1) The time it will take [min & sec] for the room to increase in temperature from 10°C to 20°C.

2) Pressure [bar(a)] in the room at the end of the process.

Assumptions:

1) No air escapes.

2) This is a quasi-equilibrium process.

3) Air behaves like an ideal gas because it is at relatively high temperature and low pressure relative to its critical point values.

4) No energy is being generated/liberated or destroyed/hidden via any process.

5) KE and PE of control volume contents are negligible.

Diagram:

Solution:

Use Reynold’s Transport Theorem to account for energy interactions affecting the control volume.

Discussion:

The shaft work was minimally contributive compared to the resistance heater and heat loss through the wall. However, the existence of the running fan made our analysis more accurate, since we assumed the contents of our control volume were homogenous, and the fan would definitely help to mix things up and not allow any internal temperature gradients.

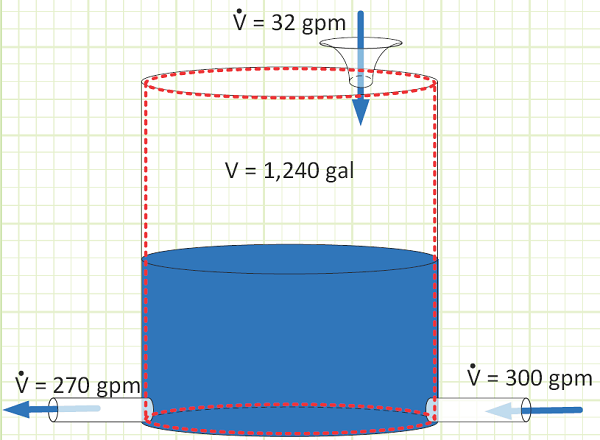
EXAMPLE 2 – TRANSIENTLY FILLING A TANK WITH AN INCOMPRESSIBLE LIQUID

Problem statement: A tank has a pipe with liquid flowing in, another pipe with liquid flowing out, and a funnel at the top through which more liquid flows in, as shown on the diagram. The time until the tank is completely filled is to be determined.

Given:

Maximum tank volume, V, is 1,240 gallons.

Liquid flows in at 300 gpm from the pipe.

Liquid flows out at 270 gpm from the pipe.

Liquid flows in from the funnel at 32 gpm.

Find:

a) The time it will take for the tank to fully fill with liquid.

Assumptions:

1) The tank is vented to atmosphere.

2) The pipe flow rates are not a function of liquid column height.

3) The liquid density does not change (is incompressible).

Diagram:

Solution:

Use Reynold’s Transport Theorem and conservation of mass to account for all mass flux:

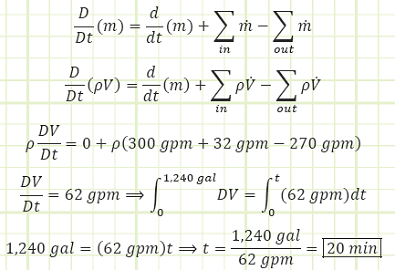
Discussion:

The overall fill rate is about 2/3 that of the handheld fire hose nozzles Coast Guard and Navy ships. 1,240 gallons is equivalent to about 166 cubic feet. The 2019 Ford Explorer has a total internal passenger cabin volume of 151.5 cubic feet. So at this net flow rate, it would take a little more than 18 minutes to completely flood a firstie’s new car.

EXAMPLE 3 – STEADY STATE OPERATION OF A TURBOPROP

Problem statement: A turboprop is consuming 40 kg/s of air with a specific energy of 0.1225 MJ/kg and expelling the same amount at 0.220 MJ/kg. Fuel is supplied to the engine at 6 MW, 1.5 MW of which is converted to shaft work to spin the propeller. How much energy is lost as heat to the surroundings if the engine’s surface temperature is not changing with regard to time?

Given:

Convection in/out of control volume.

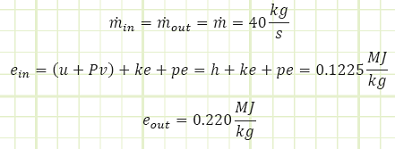
Work interactions in/out of control volume.

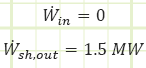
Heat interactions in/out of control volume.

Find:

The rate at which heat is shed from the engine.

Assumptions:

1) The engine is operating at steady state.

2) Fuel combustion is modeled as a heat input with no fuel mass flow.

3) The mass of combusted fuel in the mass leaving the engine is negligible.

Diagram:

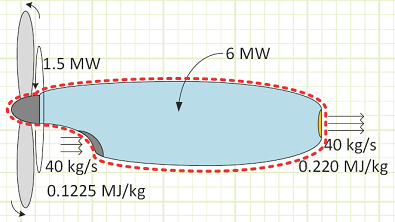
Solution:

Use Reynold’s Transport Theorem to account for energy interactions affecting the control volume.

This heat loss, 600 kW, represents 10% of the original heat input to the engine and represents higher quality energy being discharged to the surrounding environment.  The air entering the engine represents an energy input of 4,900 kW, while the hot exhaust is 8,800 kW. A typical blow dryer is about 1 kW, so this engine is the equivalent of about 8,800 personal blow dryers. An Olympic-size swimming pool is 2,500 m³, or 2.5 Mg of fresh water with a specific heat capacity of 4.18 kJ/kg°C. The total heat energy shed (9,400 kW) from this engine would change a full pool’s water temperature by 1°C in approximately 18.5 minutes.

EXAMPLE 4 – ACTIVE ATTENDANCE AT A FICTIONAL ARENA FROM A TIME OF LESS GENERAL CIVILITY

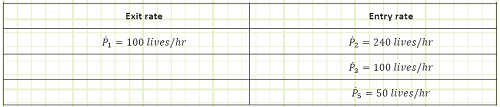
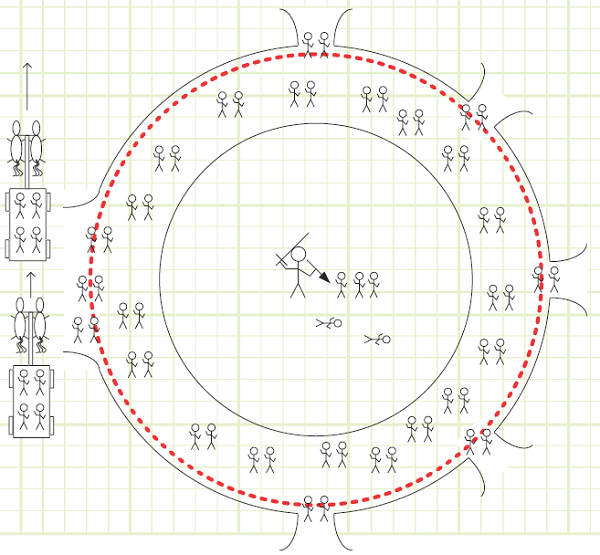
Problem statement: The official fire marshal of an ancient “sports” arena needs to keep track of how many people are inside the arena at any given time, in case it needs to be quarantined due to an outbreak of plague, small pox, diphtheria, malaria, lawlessness, dysentery, sorcery, etc. There are five street access points, labeled P₁ through P₅, as well as one chariot station, C, at which wealthier individuals are embarked and debarked by chariots arriving and departing at a rate of 30/hr. Arriving chariots bear 8 people while departing chariots take 3 people. The Fire Marshall has arrival/departure reports from all the access points except P₄. She also knows the average rate of life generation (live births minus gladiator/crowd deaths) is -5 lives/hr. 

Given:

Part A, DP/Dt = 0.

Part B, DP at t = 4 hrs = 3,000 lives.

Rates of arrival and departure at all entrances except P4, as shown in the following table.

A summary of entry and exit rates is given in the following table:

Chariot arrival and departure rates, as shown below.

Find:

a) The rate of entry at P₄ in order for the stadium’s population to remain constant.

b) The rate of P₄ if the stadium is initially empty and fills to 3,000 people in four hours.

Assumptions:

1) People exist in a mutually exclusive binary state.

Diagram:

Solution:

a) Use Reynold’s Transport Theorem to account for all entries and exits:

 b) Use Reynold’s Transport Theorem to account for all entries and exits:

Discussion:

Part (a) was a steady state scenario, where the rate of change of people within the stadium was zero, even though different people were constantly arriving/departing & dying/being born. The net outcome of all these interactions was a net of zero change with regard aggregate life content.

Part (b) was a transient scenario, as the storage term experienced a change with regard to time. It was actively growing from a population of zero to 3000.  The overall rate of change was 3000/4, or 750 arrivals per hour.

Source

Unknown Contributor - Reddit

Related:

• Introduction to Thermodynamics, Class 1
• Ideal Gas Assumptions Class 2
• FIRST LAW OF THERMODYNAMICS
• SECOND LAW OF THERMODYNAMICS
• Thermodynamic Systems and Surroundings
• Types of Thermodynamic Systems
• Thermodynamic Equilibrium
• Control Volume
• Steady State
• Thermodynamic Process
• Cyclic Process
• Reversible Process
• Irreversible Process
• Adiabatic Process
• Isentropic Process
• Polytropic Process
• Throttling Process