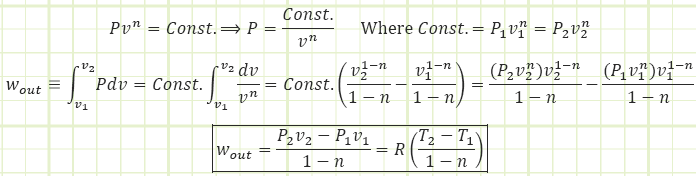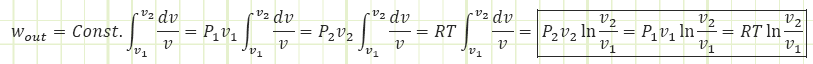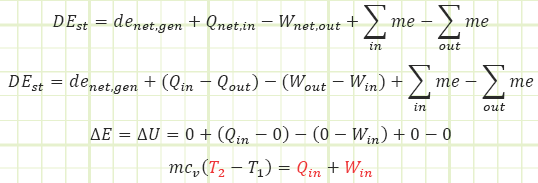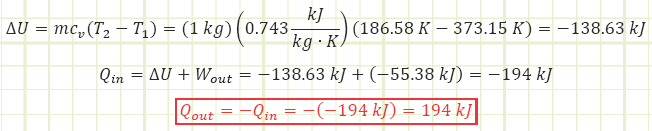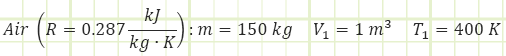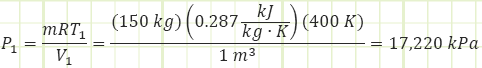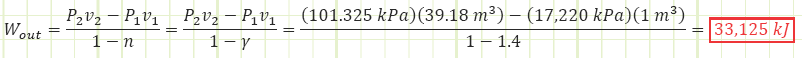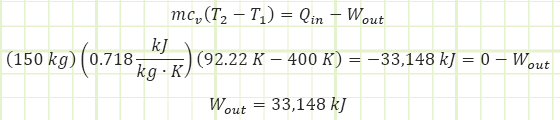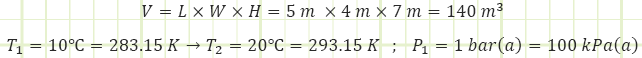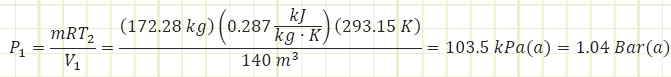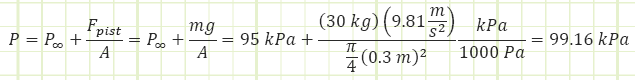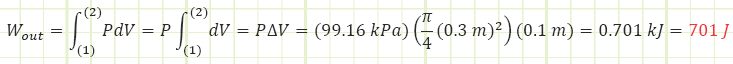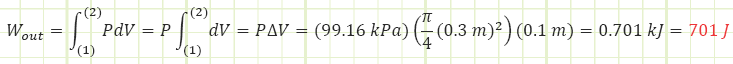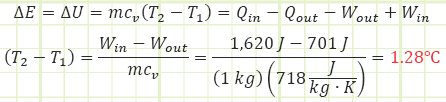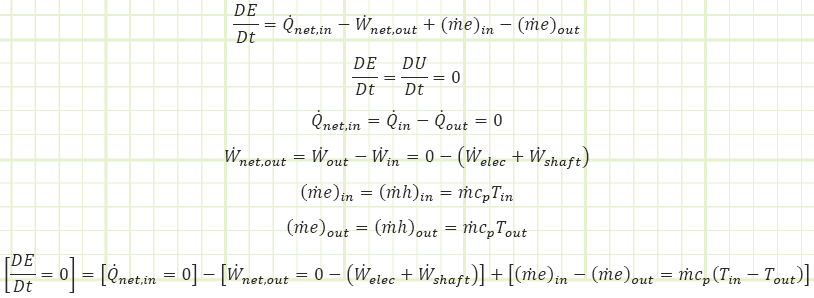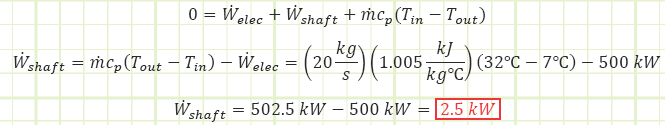Mechanical Work for Closed Systems Class 4

Related Resources: thermodynamics

Mechanical Work for Closed Systems Class 4

Thermodynamics Data, Equations, Charts, Equations and Calculators

Mechanical Work for Closed Systems - Class 4

Objective(s):

At the completion of the lecture, students should:

1) Identify the polytropic relationship, Pvⁿ = Const.

2) Identify and apply special values of “n” for specific processes.

3) Use the P-v diagram to plot processes.

4) Use the P-v diagram to determine the boundary work for a process. 5) Recognize other forms of work (electrical, shaft, paddle)

Methodology:

Lecture with simple demonstration and visual aid (ideal gas simulator, syringe).

Terminology:

Control Mass: A control volume in which mass remains constant because the control surface is impervious to the inflow and outflow of mass. Heat and work are the only permitted boundary phenomena with the surroundings. isobaric: a process during which the pressure of the control mass remains constant.

isothermal: a process during which the temperature of the control mass remains constant. adiabatic: a process during which no heat is transferred to or from the control mass.

Isochoric / isometric: a process during which the volume of the control mass remains constant.

Polytropic: a general process during which no constraints are explicitly imposed.

Path dependence: The area under a curve depends on the path taken from one point to another. There are an infinite number of ways to get from one state to another; their curvature determines the area.

Boundary work: The energy associated with pushing the surface of our control volume. An expanding gas in a cylinder-piston device pushes the piston outward (presumably against ambient pressure). A force is being applied over a distance (or a pressure applied during a change in volume), which is work.

Electrical work: The transfer of energy associated with the flow of electrons. In this class, the electrons will usually flow through a resistance heating element and release heat directly into the control system.

Shaft work: The energy associated with a torque and an angular velocity.

Paddle work: The energy given to a substance by a mixing action, such as a ceiling fan.

Mechanical equilibrium: A condition in which the pressure is equal between spatial regions. Since a pressure gradient drives the flow of matter, the absence of a pressure gradient results in no mass flow. For fluids in which head pressure due to gravity is significant, the pressure difference between elevations is exactly canceled by the difference in pressure due to gravitational potential energy.

Key Ideas:

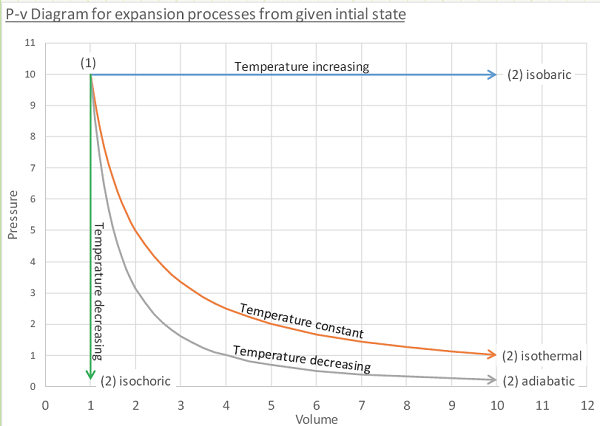
The P-v plot:

A graphical method to depict a quasi-equilibrium process in which pressure is shown as a function of (specific) volume.

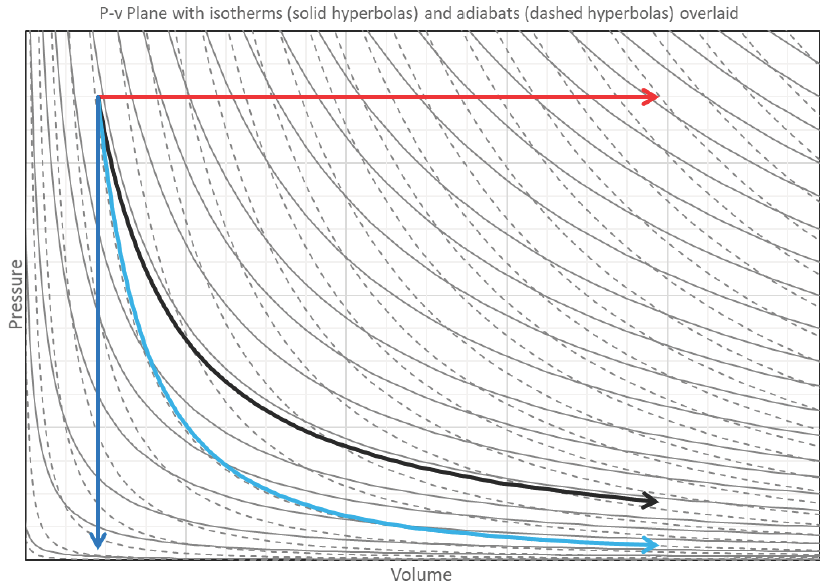
The P-v graph above has lines of constant temperature (isotherms) overlaid, in order to show the qualitative relationship between pressure, specific volume, and temperature, using the Ideal Gas Law to relate all three. If a process line crosses isotherms, then the temperature of the system is changing. In the special case of an isothermal process, the process exactly follows one isotherm, so its pressure and volume interact in a special way such that the system’s temperature doesn’t change (i.e. Pv = RT where T remains constant and P is an equilateral hyperbolic function of v → P = Const./v = P₁v₁/v = P₂v₂/v = RT₁/v = RT₂/v = RT/v).

General Polytropic process:

Isobaric process; system pressure remains constant. This can occur if heat is added or removed in order to increase/decrease temperature from one state to the next as work is performed.

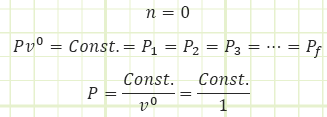
Isobaric process

Isothermal process; system temperature remains constant. This can occur if heat is added or removed in order to control temperature as work is done by or on the system from one state to the next.

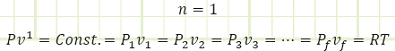
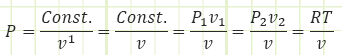
Isothermal process; system temperature remains constant

Adiabatic process; no heat is added or removed from the system as work is performed.

The same representative expansion processes (except the isochoric process can’t expand) on a P-v plot with both isotherms and adiabats overlaid. For the adiabats we assumed the specific heat capacities of the gas remain constant for all values of temperature, pressure, and specific volume, which means 𝛾 remains constant. Notice how the adiabatic process (lighter blue line) crosses isotherms: the system cools down as it expands because it’s using up its stored internal energy by converting it to boundary work.

For the isothermal process, just enough heat is added to keep the internal energy constant (because U is a function of T and only T for an ideal gas), so any heat added in the isothermal process immediately becomes work.

The isobaric process crosses a LOT of isotherms. Lots of heat is being added to increase the system’s internal energy and some of it also goes toward boundary work on the surroundings.

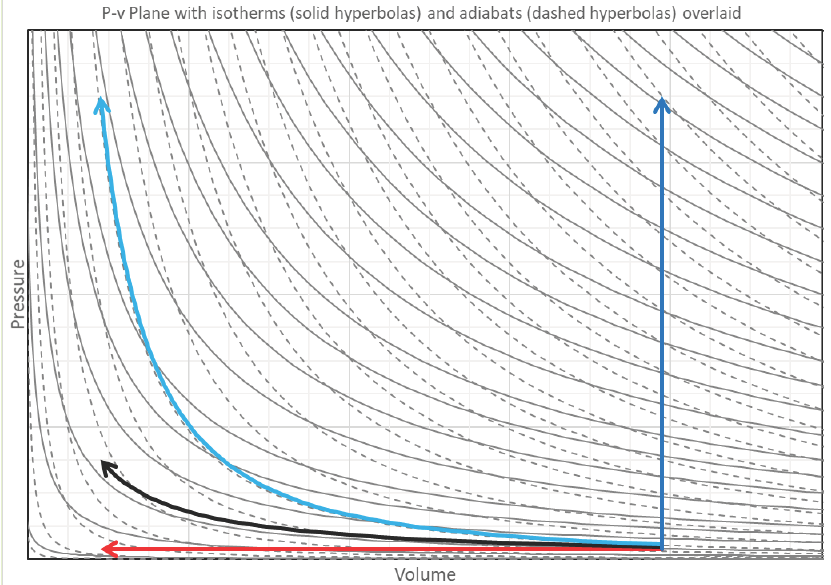
Isochoric, isobaric, isothermal, and adiabatic processes shown on the same P-v plot with isotherms and adiabats overlaid.

The area under the process path as depicted on a P-v diagram is what we care about. It represents the boundary work of the process (either the push we want FROM the control volume (W_out) in order to get work out of a process, or the energy we have to put into the system in order to compress the it (W_in). The

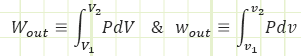
area under the process path as depicted on a P-v diagram

Where W_out is the total energy leaving the system in the form of boundary work (or entering it, in case you get a negative value, such as during a compression process from a large V to a smaller V) and w _out is the specific boundary work (i.e. how much work is performed for each kilogram of substance in the system).

Boundary work for a general polytropic process:

This relation works for all values of n except n = 1 (isothermal), which is shown next.

Boundary work for an isothermal process:

P₁ v₁ = P₂v₂ = RT₁ = RT₂ = RT = Const.because T is constant for an isothermal process

w_out is a “specific” quantity. It says how much work energy is done by one unit of mass of gas. It’s typically in units of kJ/kg or BTU/lbm. To determine the total work output in a process, multiply the specific quantity by the amount of mass in our system, w_out = mw_out. For the polytropic work output expression, we get total work [kJ or BTU] via:

Where capital V is the total volume of our system at either state 1 or state 2 (not the specific volume, which is equal to total volume divided by total mass, i.e. V/m). The total work output from an isothermal process is:

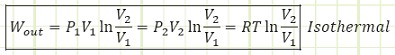
total work output from an isothermal process

When does work output happen? When the volume is expanding. Why? Molecularly?

A molecule hitting a movable boundary will impart some of its momentum and energy to that boundary, making it move outward. That boundary will push away the surroundings based on the force (i.e. momentary transfer of momentum) exerted by the molecule. The molecule has given away some of its own energy in order to cause movement, which is also known as boundary work. If that energy isn’t subsequently replenished by heating, the molecule will become “colder” (i.e. will have lower velocity) after the impact.

Why does it take work to compress the volume? Where is this work energy going?

The boundary is moving inward, compressing the molecules closer together. Every time the inward-moving boundary hits a molecule, it makes the molecule fly away faster (increasing its energy, like hitting a baseball with a bat). The boundary work is causing the internal energy of the molecules to increase by making them slam into a surface moving towards them.

Which process has no boundary work associated with it at all? Isochoric. dV = 0, so n = ∞

Starting from equivalent states, which process gives us the maximum work output when expanding from one volume to another? Isobaric, but it takes a LOT of heat, with most of it going to increasing the internal energy.

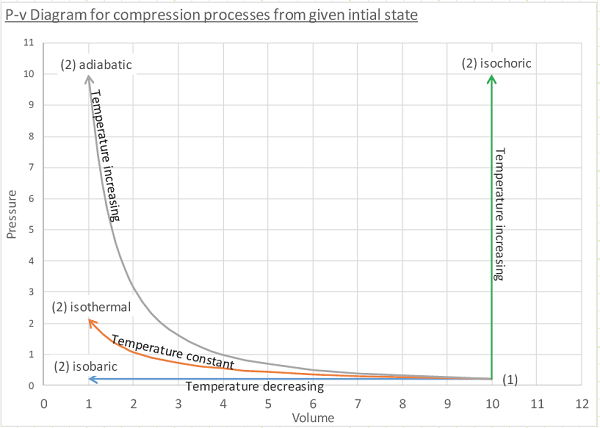
Starting from equivalent states, which process takes the most work when compressing from one volume to another? Adiabatic, but on the positive side if you were to let it expand again, you would get back ALL of the work you had to expend in compressing it in the first place without ever having to give or absorb any heat.

Say we’re compressing a gas with a compressor. What can we do to the gas as we compress it so the compressor doesn’t have to work as hard? Cool it down! Remove energy via heat transfer before or even during the compression process so it looks more like an isothermal or isobaric compression process. This is why intercoolers are installed in-line with air compressors and turbo/super chargers.

Summary:

Process	Control Property	Polytropic exponent	Heat Transfer?	Boundary work?
Isobaric	ΔP = 0	0	Yes	Yes
Isothermal	ΔT = 0	1	Yes	Yes
Adiabatic	Qin = Qout = 0	ɣ = c_p / c_v	No	Yes
Isochoric	ΔV = 0	ꝏ	Yes	No
Generic	None	Anything	Maybe	Maybe

Work energy can cross the boundary of the system in other ways, like spinning a fan inside the room using electricity or pumping electrons into the system and have them heat it via a resistance heating element. In both these cases, the work contribution to the increase of internal energy can’t be reversed and both processes essentially look and act like a heating process. But, technically, it’s considered a work interaction (just not a boundary work interaction).

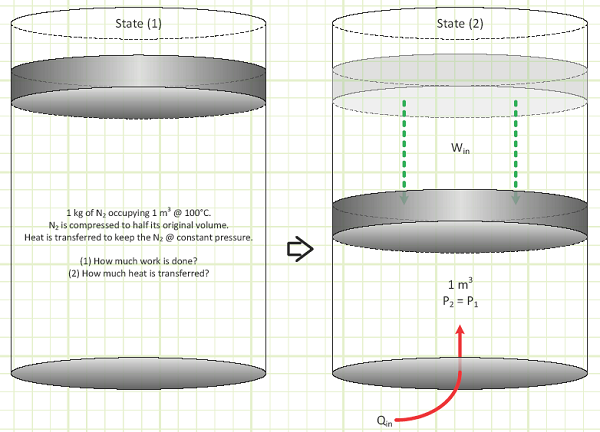
EXAMPLE 1 – ISOBARIC COMPRESSION OF NITROGEN IN A CLOSED SYSTEM

Problem statement:

1 kg of nitrogen occupies 1 m³ at 100°C. It’s isobarically compressed to half its volume. Determine the energy interactions (Boundary Work, Heat Transfer, and change of Internal Energy).

Given:

Nitrogen: m = 1 kg V₁ = 1 m³ V₂ = 0.5m³ P₁ = P₂

Find:

1) Heat transferred [kJ].

2) Work performed [kJ].

3) Internal energy change [kJ].

Assumptions:

1) Nitrogen behaves like an ideal gas. Internal energy is a function of only temperature.

2) There is no friction; quasi-equilibrium process; no mass flows in/out → no change in mass.

3) Specific heat capacity remains constant (not a function of temperature).

4) Internal energy is the only form of stored energy (Chemical, nuclear, KE & PE are nonexistent or negligible).

Diagram:

Solution:

Use Reynold’s Transport Theorem to account for energy interactions affecting the control mass.

Need to determine T₂, which can be obtained from Ideal Gas equation of state.

Need to determine pressure to get boundary work, which can be obtained from Ideal Gas equation of state.

Using the First Law energy accounting equation for a closed system, determine change in internal energy, then subtract out the energy added via boundary work.

Discussion:

194 kJ of heat had to be taken from the nitrogen in order for the volume to decrease to half its value while keeping the gas’s pressure constant. This energy is equivalent in magnitude to the kinetic energy of a 3,000 pound vehicle traveling at almost 27 MPH. As the gas cooled down and shrunk, the ambient environment pushed down on it, imparting 55.4 kJ of energy into it. Overall, the change in the nitrogen’s stored energy is equal to the work put into it minus the heat taken from it, or 55.38 kJ – 194 kJ = -138.63 kJ. This drop in stored internal energy was exhibited as a drop in temperature from 100°C to -104.6°C. For a visual demo using liquid nitrogen to cool down air in balloons, watch this: https://youtu.be/9vRMZSEF_a4

EXAMPLE 2 – UNSTEADY ADIABATIC EXPANSION

Problem statement:

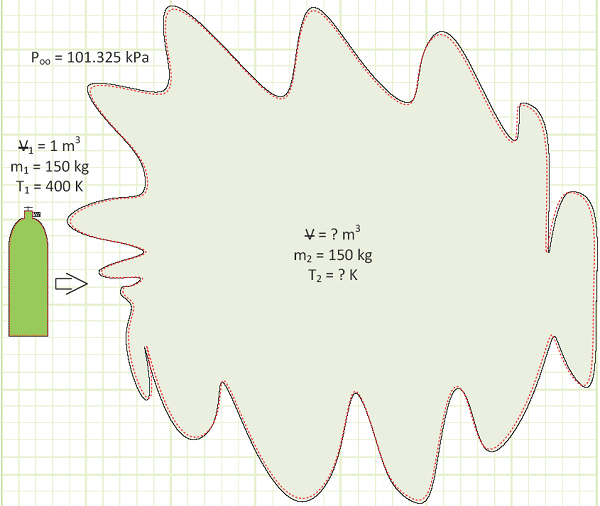
A 1 m³ cylinder storing 150 kg of air at 400 K suddenly explodes on a ship. It occurs too quickly for heat to be transferred to the gas. How much boundary work energy [kJ] is associated with the explosion?

Given:

1) Boundary work of the expanding gas.

Assumptions:

1) Explosion is quasi-equilibrium (unrealistic, but simplifies things).

2) Air behaves like an ideal gas; internal energy is a function of only temperature.

3) Specific heat capacity remains constant.

4) No mixing w/ surroundings at the boundary of the system. This is a closed system with an expanding boundary.

5) Ambient pressure is 101.325 kPa.

Diagram

Solution:

Use ideal gas law to determine initial pressure inside the air bottle.

Use polytropic relationship to determine final volume of the gas once it has expanded enough to match the ambient pressure. Assume the expansion occurs adiabatically, so n = γ = 1.4 for air.

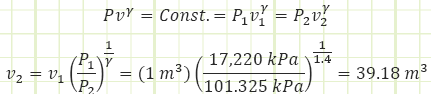
polytropic relationship to determine final volume of the gas

Use polytropic relationship to determine the boundary work done by the gas as it expands against the atmosphere. This is the energy liberated during the explosion.

Discussion:

Dynamite typically contains about 1 MJ of energy per stick. Therefore, this is about 33 sticks of dynamite. How realistic is this expansion? Does air remain an ideal gas? To what temperature does it drop during the expansion? From the ideal gas law:

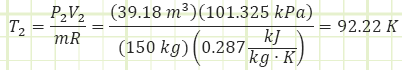
Dynamite typically contains about 1 MJ of energy per stic

This is only 15°C warmer than Nitrogen’s boiling point and colder than the critical temperature of 126.2 K.

This is only 13°C warmer than Oxygen’s boiling point and colder than the critical temperature of 154.6 K.

From these two facts, modeling the air as an ideal gas has serious issues, and it probably won’t expand to the full volume calculated using the adiabatic relationship in such a rapid time, as the pressure may plummet more precipitously as the gas approaches more of a saturated vaporous state. Still, one can expect the explosion to be violent as the compressed air molecules rapidly try to equalize with the relatively uncompressed surroundings. Since there is no heat transfer to or from the expanding gas, the boundary work exactly equals the drop in the system’s internal energy, hence why the temperature plummeted to cryogenic levels. The alternate analysis shown below would have determined the 33,125 kJ:

The slight difference in W_out values is due to significant digits and rounding error when using c_v and R versus γ = 1.4.

EXAMPLE 3 – TRANSIENT ISOCHORIC HEATING OF A SEALED ROOM

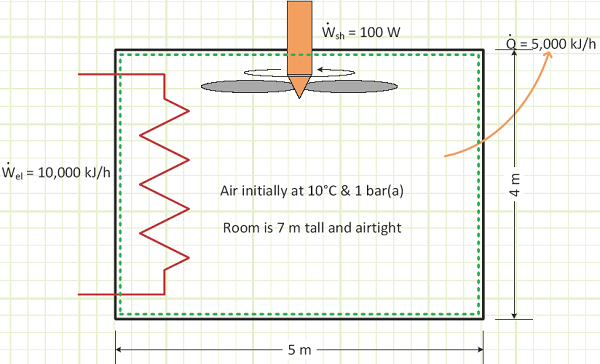
Problem statement: A sealed room containing air at 1 bar(a) is initially at 10°C. There is a fan running at 100 W, a resistance heater rated for 10,000 kJ/h, and imperfect insulation allowing heat to escape at a rate of 5,000 kJ/h. The room is 4 m x 5 m x 7 m. How long will it take [min & sec] for the air temperature to reach 20°C? What is the final pressure [kPa]?

Given:

Work interactions in/out of control volume.

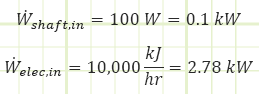
Heat interactions in/out of control volume.

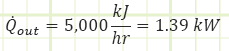
Room geometry and contents.

Find:

1) The time it will take [min & sec] for the room to increase in temperature from 10°C to 20°C.

2) Pressure [bar(a)] in the room at the end of the process.

Assumptions:

1) No air escapes.

2) This is a quasi-equilibrium process.

3) Air behaves like an ideal gas.

4) No energy is being generated/liberated or destroyed/hidden via any process.

5) KE and PE of control volume contents are negligible.

Diagram:

Solution:

Use Reynold’s Transport Theorem to account for energy interactions affecting the control volume.

Discussion:

The shaft work was minimally contributive compared to the resistance heater and heat loss through the wall. However, the existence of the running fan made our analysis more accurate, since we assumed the contents of our control volume were homogenous, and the fan would definitely help to mix things up and not allow any internal temperature gradients.

EXAMPLE 4 – TRANSIENT TEMPERATURE RISE OF AN ISOBARICALLY EXPANDING GAS DUE TO SHAFT WORK

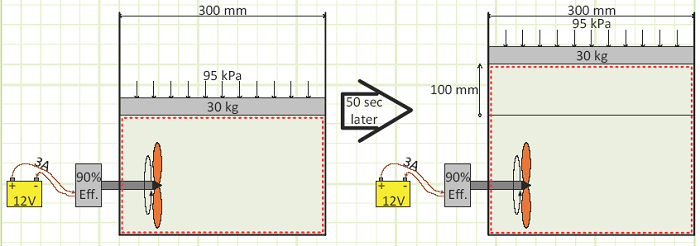
Problem statement: A sealed vessel with a frictionless sliding piston contains gas and a paddle wheel attached to a shaft spun by an external motor powered by a battery. The piston is found to have risen after a short time.

Given:

Vessel diameter = 300 mm

Piston mass = 30 kg

Battery is 12V, current is 3A, motor is 90% efficient Ambient pressure = 95 kPa.

Piston rises 100 mm in 50 seconds.

Find:

1) Work done by the gas [J].

2) Shaft power [W] and energy imparted [J] by the motor.

3) The temperature change of the gas if it is 1 kg of air [°C].

Assumptions:

1) Gravity is 9.81 m/s².

2) Closed system.

3) Unsteady (transient) conditions.

4) c_v,air is constant at 0.718 kJ/kg*K.

5) The vessel is thermally insulated.

Diagram:

Solution:

Determine the pressure inside the control mass.

Use the expression for isobaric boundary work to determine the work done by the gas:

Use the expression for electrical power to determine the shaft power and energy of the paddle:

Use Reynolds Transport for conservation of mass to determine the final temperature of the gas:

Discussion:

The paddle wheel essentially acted like a resistance heater or a heat transfer. All the paddles did was impart energy to the gas, causing its internal energy to increase. Had the control volume been rigid, its temperature would has risen more than what was determined. The lower temperature rise is due to some of the gas’s internal energy being converted into boundary work, pushing the piston up against ambient pressure and gravity. If boundary work is the desired output of this process, then the efficiency of the gas in raising the piston is 701 J / 1620 J = 0.43. Including the motor’s efficiency, 0.9, the overall efficiency of the apparatus is (0.9)(0.43) = 0.39. Any energy not being used to raise the piston just contributes to raising the temperature.

EXAMPLE 5 – STEADY STATE ENERGY INPUT TO CAUSE A RISE IN TEMPERATURE

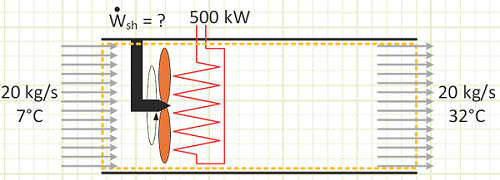
Problem statement: Outside air at 7°C is drawn through a ventilation duct at 20 kg/s by a fan. A heater that provides 500 kW of energy is installed in the duct. The air exits the duct at 32°C. What is the power rating of the fan (kW) while the heater is running?

Given:

Air temperature: T₁ = 7°C → T₂ = 32°C

Heater energy input rate: W_elec,in = 500 kW

Air mass flow rate: m_air = 20 kg / s

Find:

Power rating of the fan to help cause the observed temperature change.

Assumptions:

1) System operates at steady state.

2) Air is an ideal gas.

3) Specific heat remains constant (not a function of temperature).

4) The duct is thermally insulated.

5) Kinetic and potential energy of the flow is negligible.

Diagram:

Solution:

Use Reynolds Transport to account for energy changes taking place.

Discussion:

How much of the temperature rise was due to the heater? Use a smaller control volume and pretend the heater is upstream of the fan. The 500 kW heater caused the air’s temperature to increase by 24.88°C to 31.88°C. The shaft work from the fan caused the remaining 0.12°C increase in order to reach 32°C. Had the fan been much more powerful, the kinetic energy imparted to the air flow via the fan blades would probably be significant and would need to be accounted for in the analysis.

Source

Unknown Contributor - Reddit