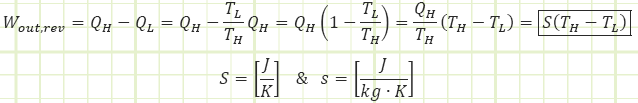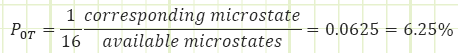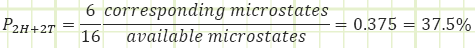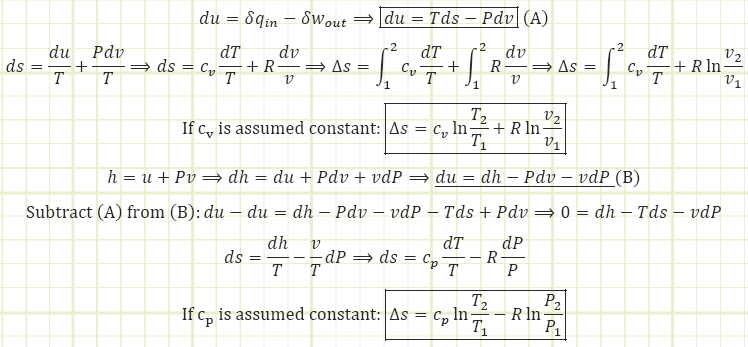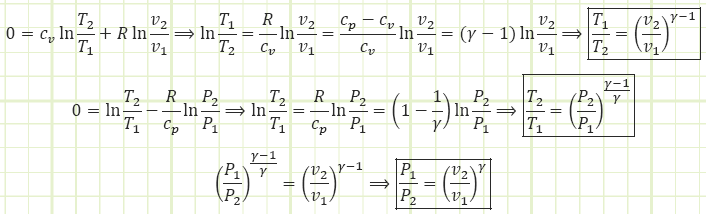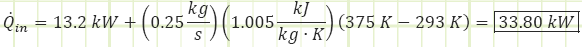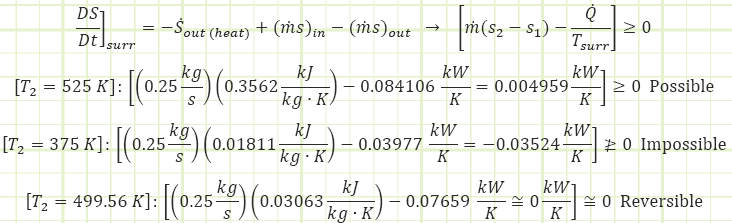Closed System Cycles Thermodynamics – Carnot Cycle & Entropy Class 10

Related Resources: thermodynamics

Closed System Cycles Thermodynamics – Carnot Cycle & Entropy Class 10

Thermodynamics Data, Equations, Charts, Equations and Calculators

Closed System Cycles Thermodynamics – Carnot Cycle & Entropy Class 10

Objective(s):

At the completion of the lecture, students should:

1) Understand the meaning of the terms “reversible,” “internally reversible,” and “totally reversible” as pertaining to thermodynamic processes and cycles.

2) Understand the typical sources of irreversibility with regard to processes.

3) Understand the working principle of a theoretical Carnot heat engine.

4) Identify how the property Entropy pertains to a fully reversible cycle.

5) Recognize the Clausius Inequality and apply it to the Increase in Entropy principle.

6) Recognize the equivalence between irreversibility, entropy generation, and lost work potential.

7) State the Kelvin-Planck and Clausius statements of the Second Law of Thermodynamics.

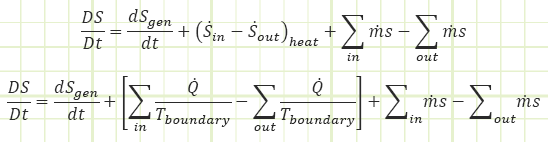
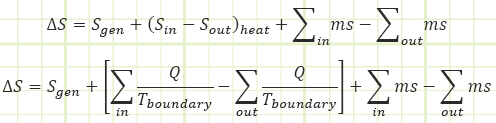
8) Use Reynold’s Transport Theorem to account for entropy transfer to/from a system and entropy generation within the system.

9) Use values of S_gen to determine when a process or cycle is: 1) possible or impossible and 2) reversible or irreversible.

10) Apply property relations to determine properties at states bounding isentropic processes.

11) Recognize how entropy is a property that measures the degree of molecular “disorder” or “uncertainty” of a system at some state relative to a different reference state.

Methodology:

Lecture with supplemental video (1 ,2 ,3 ).

Terminology:

Reversible: A process that can be reversed (completely undone) without leaving any trace on the surroundings. If you compress an ideal spring, you do work on it and lose some of your own energy. But that spring can give that energy right back, also in the form of work. Ideal springs are reversible.

Internally-reversible: When no irreversibilities occur within the boundaries of the system during a process. Irreversibilities may still be occurring outside the system’s boundaries.

Irreversibility: Friction, unrestrained expansion, mixing of two fluids, heat transfer across a finite temperature difference, electric resistance heating, inelastic deformation of solids, chemical reactions. These can’t be undone without expending work. The energy consumed to overcome friction when pushing a book across a desk isn’t stored for later use; that energy will never push the book back in your direction. That work energy has been forever degraded to disorganized molecular jiggling (heat).

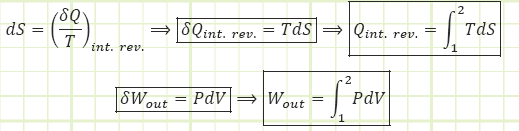
Isothermal heat transfer: When infinitesimal quantities of heat, 𝛿𝑄, are transferred across a differential temperature difference, dT.

Temperature reservoir: A thermal energy source or sink such that addition or removal of heat from it does not change its temperature (i.e. reservoir temperature remains constant either because it’s huge or its undergoing a phase change).

Kelvin-Plank Statement of the 2^nd Law: It is impossible for any device that operates on a cycle to receive heat from single reservoir and produce a net amount of work.

Clausius Statement of the 2^nd Law: It is impossible to construct a device that operates in a cycle and produces no effect other than the transfer of heat from a low-temperature body to a higher-temperature body.

Key Ideas:

Carnot cycle:

A sequence of four totally reversible processes applied to a control mass or control volume in which the end state and beginning state are identical.

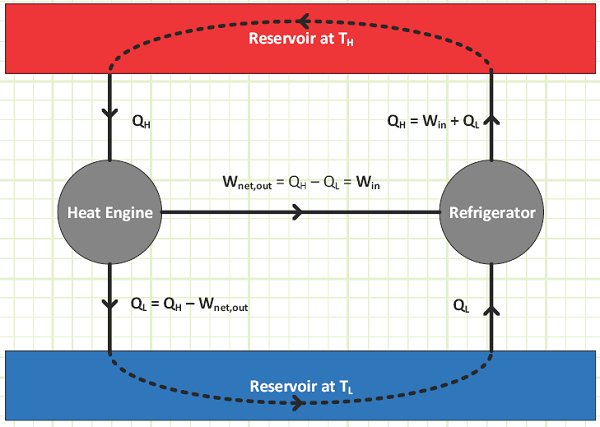
Can run “forward” as a heat engine operating between two steady temperature reservoirs, producing useful net work output at the completion of every cycle. Can also run “backwards” as a refrigerator into which work is exerted in order to transfer heat from a source at low temperature to a sink a higher temperature. Schematically, the heat engine and refrigerator can be depicted as:

The heat engine net work output and refrigerator work input for totally reversible devices operating between the same two reservoirs is EXACTLY the same, such that the heat engine could power a refrigerator to create a “heat loop” in which there is no net change on the overall condition of either reservoir (or the universe).

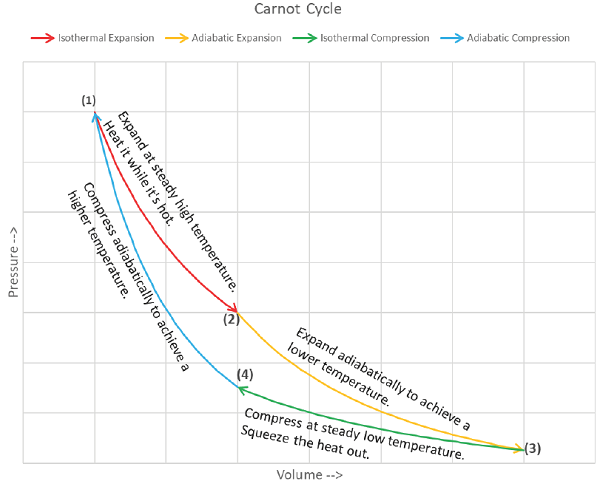
There are four totally reversible processes comprising the Carnot Power Cycle:

1) Isothermal Expansion (State 1 to State 2): An ideal gas is initially at temperature T_H. Heat is gradually added via infinitesimally tiny amounts, δQ_in, from a thermal reservoir also at temperature T_H as external pressure on the piston is reduced very slowly, which permits the gas to perform differential amounts of work, δW_out, on the piston. When the gas does a differential amount of work on the piston, its internal energy will decrease by a differential amount dU, and since internal energy is a function of only temperature for an ideal gas, its temperature accordingly drops by dT. Now, a temperature difference between the reservoir at T_H and the gas, which is (T_H - dT), exists. Heat therefore will flow from the reservoir to the gas, restoring its temperature to T_H, at which point the process occurs all over again and proceeds until pressure has been reduced to some intermediate amount and volume has increased. The total amount of work output by the piston during this expansion is exactly equal to the heat input, since the internal energy of the gas at state 2 is identical to what it was at state 1 (i.e. same temperature).

2) Adiabatic Expansion (State 2 to State 3): External pressure is further reduced, but this time the cylinder is not in contact with any thermal reservoir, so the internal energy of the gas decreases as it performs work on the piston. This process proceeds until the gas temperature has dropped to T_L.

3) Isothermal Compression (State 3 to State 4): Similar to the isothermal expansion process, the external pressure is now increased very slowly, which does work on the gas, infinitesimally raising its internal energy and temperature by an amount dT, so it is T_L + dT. The cylinder was placed in thermal contact with a reservoir held at T_L upon reaching State 3 and the temperature difference between it and the gas allows heat, δQ_out, to flow from the gas to the reservoir. Basically, the external pressure is slowly “squeezing” the heat out whereas it “sucked” the heat in during the isothermal expansion process.

4) Adiabatic Compression (State 4 to State 1): The cylinder is again thermally isolated and the external pressure continues to increase. Since the gas can’t shed its excess energy anywhere anymore, its temperature increases as the external pressure does work on the gas. This proceeds until its volume and pressure are the same as they were when the first process started at state 1.

For isothermal processes, the heat input (output) is equal to the work output (input):

This formula for thermal efficiency applies to ANY totally reversible heat engine, not just a Carnot heat engine.

Has profound and far-reaching implications. It requires, for a certain amount of heat rejected to a colder sink at a given temperature, an exactly defined amount of heat must be absorbed by a reversible heat engine based on the temperature at which it is taken in. Since w_{net, out} = q_in - q_out, if the sink temperature, T_L, is defined, and the heat rejected to it, q_L,is known to be some specified amount, then based on a measured amount of net work from the reversible engine, we can then know the temperature of the source, T_H.

This is how the thermodynamic temperature scale is defined. If we define T_L to be 1 absolute unit of temperature (like 1 Kelvin or 1 Rankine), we can determine all other temperatures above this unit temperature by measuring (or hypothesizing) the amount of work that would come out of a reversible heat engine when heat is taken from a reservoir at T_H. This work could be used to move the needle of a gauge or to raise a weight against the pull of gravity to indicate the absolute magnitude of T_H.

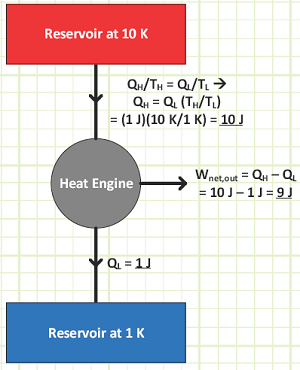
thermodynamic temperature scale is defined

If 7 energies of heat is rejected to the unit temperature sink [1° B] and 333 energies of net work output is obtained, what is the temperature of the source and how much heat did the engine accept from this reservoir?

This works for any unit of energy (even made-up ones) and allows us to DEFINE our OWN temperature scale.

No engine can outperform a reversible engine and every reversible engine will perform the same, regardless of how each individual one is made or the processes within the cycle it performs. This is a FUNDAMENTAL law of physics and defines the limit of how much heat can be converted into work or how much work it takes to transfer heat from a lower temperature reservoir to a higher temperature reservoir.

Just like a gas contained at high pressure can expand (and do work) only until its pressure matches the ambient pressure, high temperature energy can push only until its temperature matches the colder surroundings, at which point there’s no longer a “potential” permitting/causing the flow of that energy.

A weight held 10 meters above the ground can only fall until it hits the ground. If that weight is attached to a shaft spinning a fan or turning the gears of a clock, it will only provide energy for as long as it can fall. Once it reaches the ambient ground elevation, its capacity to do work ceases, even if it still has significant energy relative to, say, the center of the earth. Unfortunately, the ground is in the way, so the center of the earth is offlimits.

So now we see there is thermal potential in much the same way as there is gravitational potential or pressure differential potential. The “ground state” is as low as we can go, and T_L is the ground state for temperature. Usually, that’s the temperature of the ambient environment (like the ocean).

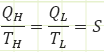
thermal potential

Here, “S” is the Entropy associated with the transfer of heat into or out of our reversible engine. Just as much entropy enters our reversible engine from the higher T reservoir as leaves when it goes into the lower T reservoir. S represents the amount of work that could be done by a reversible heat engine operating between two temperature reservoirs:

Entropy is a property, albeit not one we can measure directly like Temperature or Pressure. It is a measure of how much molecular uncertainty exists at one state relative to some universal reference state at which entropy = 0. This zero-state occurs at 0 K in a crystalline solid (Third Law of Thermodynamics).

The T-s Diagram

T-s Diagram

Molecular Uncertainty:

Say we have four individual coins, each with two distinct states, heads or tails. How many ways can we have 0 tails, 1 tail, 2 tails, 3 tails, and 4 tails?

Macrostate	Microstates						# of Microstates
4H + 0T			HHHH				1
3H + 1T		HHHT	HHTH	HTHH	THHH		4
2H + 2T	HHTT	HTHT	THHT	HTTH	THTH	TTHH	6
1H + 3H		TTTH	TTHT	THTT	HTTT		4
0H + 4T			TTTT				1

So there are a total of 16 available microstates, each of which has equal likelihood of occurring. So what is the probability we’ll have no tails at all, corresponding to a macrostate of 4H + 0T?

What about a macrostate of 2H + 2T?

We are 6 times more likely to exist in a macrostate of 2H + 2T (which has six possible microstates) than we are for a macrostate 4H + 0T (which has only one possible microstate). Therefore, we’d expect to see the 2H + 2T macrostate occurring far more often.

What if we have 100 coins? The probability of having zero tails and 100 heads is 7.9 ∙ 10⁻³¹ (7.9 ∙ 10⁻²⁹ %). Conversely, 50H + 50T accounts for 0.08 (8% chance). There’s a 70% chance of having somewhere between 45 and 55 Heads yields. The more “ways” there are of having a particular macrostate, the less certainty we have in predicting how the coins are ordered, because there are so many available microstates corresponding to that macrostate. What about when there’s 10¹⁶ coins, just as there are approximately 10¹⁶ molecules of air in one cubic millimeter of ambient air? Entropy is a direct measure of this uncertainty:

S = k ln Ω

Where k is the Boltzmann constant and Ω is the number of available microstates for a given macrostate. The macrostate corresponding to the maximum value of Ω results when the system is said to be at maximum entropy and has therefore reached complete equilibrium with itself. It is maximally “jumbled up.” This is the way nature will spontaneously go. Nature tends toward the macrostate of most disorder (i.e. most available microstates) because there are just so many more of them than there are of the microstates where some kind of internal bulk motion driving potential exists. It’s why equipment breaks and why cutters need constant preventative maintenance (there’s only one way to have a perfectly working engine, but there are virtually infinite ways to have a broken engine). It’s why fire readily converts fuel into CO₂ and H₂O, but CO₂ and H₂O will virtually never spontaneously morph into fuel unless an outside influence forces them to via careful manipulation and expenditure of work.

Entropy Increase Principle:

The best process we can ever hope to achieve is a fully reversible process. We could “CTRL-Z” the universe to restore things to the way they were and the universe wouldn’t have any permanent mark on it. But no real process is 100% reversible; therefore, every single thing that happens will cause the entropy of the universe to increase to some maximum value, at which point total equilibrium has been achieved and microstate uncertainty is maximized. The increase of entropy principle can be demonstrated by a series of irreversible heat engines powering reversible heat pumps. The heat pumps try to “undo” the effects of the heat engines that came before them, but they can only do so much (limited by the Carnot refrigeration cycle). Each successive heat engine receives less and less heat at higher temperature and eventually it gets to the point they’re producing virtually no work output. All of the heat that was originally sucked from the high temperature reservoir has made its way permanently down to the low temperature reservoir where it’s now basically useless. Notice how the overall change on the universe was to decrease the high T reservoir’s entropy by 1 J/K, while the low temperature reservoir had its increase by 75 J/K. Taken to an infinite number of engines and heat pumps, it would increase to 100 J/K, for an overall net effect of +99 J/K of entropy gained by the universe.

S_L,tot = 30 J/K – J/K + 21.21 J/K – J/K + 15.00 J/K – J/K + 10.60 J/K = +75.25 J/K

Irreversible effects cause entropy to be generated. I personally prefer to think of it as potential (or future) entropy that has been permanently liberated (or realized). No known process can ever negate entropy that has been generated (…liberated…realized…) by an irreversible process. There is an upper limit to entropy (i.e. when total equilibrium sets in), but we’re not there yet. But all irreversible processes get us incrementally closer to reaching that state of Universal Heat Death. The forward arrow of time passage seems to be linked to the continual increase of entropy in the universe. Time occurs because processes occur; in an equilibrated universe there can be no more processes and therefore no more time.

The Clausius Inequality:

For any system undergoing a cycle, the following cyclic integral holds true:

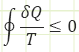
Clausius Inequality

When the sum of all the differential quantities of heat received or rejected by the system at corresponding boundary temperatures equals zero, then the cycle is fully reversible and just as much entropy went in as came out.

However, when more entropy comes out of the device than went into it, then some entropy was generated by the cyclic system and the integral is less than zero. The universe is ALWAYS receiving more entropy from its constituents than it’s offering to them. So, S_gen is ALWAYS at least zero, it’s NEVER negative.

Entropy generation is the measure of a process’s irreversibility. It correlates to “lost work potential,” i.e. the useful work we could have gotten from a process, but didn’t because of things like friction or heat transfer through a finite temperature difference. Some people call if Exergy destruction.

That’s all very interesting and scary; how is this useful to us engineers?

First, it places an upper limit on how thermally efficient our heat engines and refrigerators can be. We can’t outperform a Carnot engine. Anyone who claims differently is either a fraud or desperately in need of a Nobel Prize.

Second, it’s a property that can help us determine the state of a system, especially after it’s undergone a process from a completely known initial state. If the process is adiabatic and reversible (i.e. isentropic), then the entropy of the system didn’t change. If entropy can be related to other properties like P, v, T, u, h, etc. (and it can), then we can determine those other properties provided we at least know one of them in addition to the value of entropy. We can keep track of entropy within our system via Reynold’s Transport:

Rate equation:

Process equation:

Reversible Processes:

First Law for Energy (Closed System, internally reversible process, KE & PE negligible):

Many steady flow devices like pumps, turbines, compressors, nozzles, and diffusers operate nearly isentropically and are usually modeled as isentropic, i.e. just as much entropy exits as went in and s_out = s_in & s_gen = 0. The following three VERY USEFUL relations can be derived to relate P, T, and v between beginning and end states when an isentropic process has occurred:

For liquids and solids, which are assumed to be incompressible, the change in entropy equation is simpler:

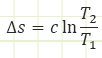
entropy equation

Keep in mind we required specific heat capacity to remain constant and we MUST be using absolute temperatures.

EXAMPLE 1 – IS THIS ENGINE EVEN POSSIBLE?

Problem statement:

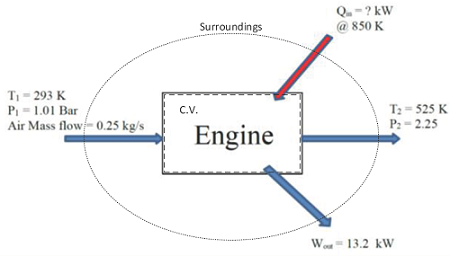
A schematically-given heat engine is to be analyzed for feasibility with regard to the First and Second Laws of Thermodynamics.

Given:

Properties at inlet:

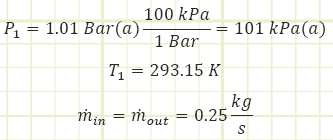
Properties at exhaust:

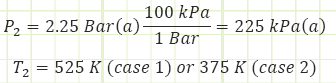
Properties at exhaus

Performance characteristics:

Performance characteristics

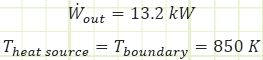
Find:

1) The rate of heat transfer, Q_in, in [kW].

2) Determine if the engine is possible by considering assumption (1) and the Second Law of Thermodynamics.

3) The same amount of power output can be produced by an engine receiving less heat input. Analyze this claim if the exit temperature is 375 K by finding a new value for Q_in.

4) Determine if the engine claimed in (c) is a possible configuration.

Assumptions:

1) Conditions are steady state (i.e. mass, energy, and entropy content of the control volume remains constant).

2) Air is the working fluid and it behaves like an ideal gas with constant specific heats; k=cp/cv.

3) Heat is being transferred into the engine from a temperature source at 850 K, which is also the boundary temperature of the immediate surroundings.

4) Kinetic and potential energies are negligible.

Diagram:

Solution:

1) Use the First Law of Thermodynamics to account for all energy exchanges, with the engine as the control volume.

2) Use the Second Law of Thermodynamics to account for entropy exchanges and creation, with the engine as the control volume.

From the perspective of the combined system, incorporating the contents of the universe (engine and its infinite surroundings), there is a net increase in the amount of entropy at a rate of 4.96 W/K. This entropy is being generated by the engine and its energy interactions and represents the lost potential to conduct useful work with the heat being added (i.e. there is excess heat energy being added to the engine that could be used for useful work, but isn’t). This alone is not reason enough to disprove the possibility of the engine as given.

3) Use the First Law of Thermodynamics to account for all energy exchanges with the new exit temperature, with the engine as the control volume.

4) Use the Second Law of Thermodynamics to account for entropy exchanges and creation, with the engine as the control volume.

The engine would need to be acting as either an active entropy storage or entropy destruction device in order for the dS/dt term to be less than zero. Since it is given that there is no change in the amount of entropy being stored in the engine, and it is impossible to destroy entropy, then it can be concluded that this second engine is impossible because it violates the Clausius Inequality of the second Law of Thermodynamics:

S_gen ≥ 0

Discussion:

At an exit temperature of 499.56 K, the entropy generation term tends toward zero, indicating the breakpoint between a possible and an impossible engine. With this configuration, the heat input is 65.10 kW, indicating an efficiency of 0.2028. Furthermore, if no entropy is being actively generated or stored, then the engine is operating in a fully reversible condition. As such, with a power input equivalent to the given power output, the engine would be capable of refrigerating the air from 499.56 K to 293 K while simultaneously discharging the removed heat to a sink at 850 K at a rate of 65.10 kW.

An alternative way of viewing the problem would be an entropy balance for the surroundings:

Reversible

Where:

represents the net entropy production rate for a universe containing only the engine. This value must at all times be greater than or equal to zero. The engine absorbs entropy from the universe by the mechanisms of heat transfer and convection and introduces entropy back to the universe through its convected exhaust flow. If this exhaust does not contain at least as much entropy as that contained in the heat transfer and intake air, the steady state engine represents an impossible configuration.

Source

Unknown Contributor - Reddit